Kapitel 3 – Relationen und Funktionen

Funktionen kennen Sie wohl alle noch aus der Schule. Dort haben Sie vermutlich die quadratische Funktion, die Logarithmusfunktion, Sinus und Cosinus sowie die Exponentialfunktion kennengelernt. Doch was sind Relationen?

Tatsächlich sind Relationen das allgemeinere Konzept. Am anschaulichsten wird dies im Bereich der Datenspeicherung deutlich. Sie haben vielleicht schon einmal etwas von relationalen Datenbanken gehört.

Diese bedienen sich genau des Konzepts der Relationen.

Eine relationale Datenbank ist eine Sammlung von Relationen. Relationen selbst kann man sich als Tabelle vorstellen:

Name	Geburtstag	Wohnort	Matrikelnummer
Karl Hecht	01.05.2000	Berlin	223323
Claudia Pech	04.02.1999	Brandenburg	223954
…	…	…	…
…	…	…	…

Wie wir dieses Konzept formalisieren, lernen wir in den nächsten Kapiteln.

Nachdem wir uns intensiv mit dem Begriff der Relation auseinandergesetzt haben, führen wir den spezielleren Begriff der Funktion ein und lernen wichtige Eigenschaften von Funktionen wie die Bijektivität kennen.

3.1 Lernziele

In diesem Abschnitt lernen wir die folgenden Dinge:

• Definition einer Relation

• Wichtige Eigenschaften binärer Relationen

• Darstellung binärer Relationen

• Definition einer (totalen) Ordnung

• Definition einer Funktion

• Definition von injektiv, surjektiv, bijektiv

Lernziele

• Studierende können eigene Relationen bilden und entscheiden, ob es sich bei gegebenen Mengen um Relationen handelt.

• Studierende können binäre Relationen graphisch darstellen.

• Studierende können sicher mit Eigenschaften binärer Relationen umgehen und entscheiden, ob gegebene Relationen gewisse Eigenschaften besitzen.

• Studierende können Ordnungen als binäre Relationen auffassen und zu einer gegebenen Relation entscheiden, ob es sich um eine Ordnung handelt.

• Studierende verstehen die Definition und die Schreibweise für eine Funktion und können diese auch als Relation interpretieren.

• Studierende können entscheiden, ob gegebene Funktionen injektiv, surjektiv oder bijektiv sind.

3.2 Relationen

In diesem Kapitel definieren wir den Begriff der Relation mathematisch exakt und veranschaulichen ihn mithilfe von Tabellen. Im zweiten Teil betrachten wir insbesondere binäre Relationen und einige wichtige Spezialfälle.

3.2.1 Allgemeine Relationen

Wir haben in der Einleitung bereits versucht, die Relation als Tabelle zu motivieren. In einer Tabelle besteht die erste Zeile meistens aus den Kategorien, die wir betrachten. In unserem Beispiel: Name, Geburtstag, Wohnort und Matrikelnummer. Kategorien interpretieren wir als Mengen, wobei die Kategorie der Namen die Menge aller Namen, die potenziell auftreten können, ist (z. B. ein Auszug aller Meldeämter). Die Menge der Matrikelnummern enthält alle validen Zahlenkombinationen, die eine Matrikelnummer bilden usw.

Sagen wir also, wir haben unsere Kategorien in Mengen \(A_1,\dots,A_n\) übersetzt.

Was ist nun eine Zeile in dieser Tabelle? Es ist eine Liste von Werten

(Karl Hecht, 01.05.2000, Berlin, 223323)

Dieses Tupel ist ein Element des kartesischen Produkts \(A_1 \times \dots \times A_n\).

Damit ergibt sich die formale Definition einer Relation wie folgt:

Definition 20

Seien \(A_1,\dots, A_n\) Mengen. Eine \(n\)-stellige Relation \(R\) ist definiert als eine Teilmenge

\[R\subset A_1\times \dots \times A_n.\]

Sind alle \(A_i\) identisch, so heißt \(R\) auch homogen, ansonsten heterogen. Für eine \(n\)-stellige homogene Relation \(R\subset A\times\dots\times A\) heißt \(A\) auch die Grundmenge.

Example 23

Sei \(A_1=\left\{0,1\right\}, A_2=\left\{0,1,2\right\},A_3=\left\{0,1,2,3\right\}\).

Dann sind folgende Mengen 3-stellige Relationen:

• \(R_1=\left\{(0,1,2),(1,2,3)\right\}\subset A_1\times A_2 \times A_3\)

• \(R_2=\left\{ (x,y,z)\in A_1\times A_2 \times A_3 \ \vert \ x+y+z=3\right\}\subset A_1\times A_2 \times A_3\)

• \(R_3=\left\{ (x,y,z)\in A_1\times A_2 \times A_3 \ \vert \ x=0\right\}\subset A_1\times A_2 \times A_3\)

Aufgabe

Geben Sie \(R_2\) und \(R_3\) in aufzählender Form an!

3.2.2 Binäre Relationen

Der Fall \(n=2\) ist ein wichtiger Spezialfall. Deshalb verdient er eine eigene Definition.

Definition 21

Eine zweistellige Relation \(R\subset A_1\times A_2\) nennen wir auch binäre Relation. Falls \((a_1,a_2)\in R\), so schreiben wir auch \(a_1Ra_2\).

Example 24

Wir definieren eine Relation \(R\subset \mathbb{R}\times \mathbb{R}\) wie folgt:

\[R=\left\{(x,y)\in \mathbb{R}\times \mathbb{R} \ \vert \ x<y \right\}\]

Wir nennen diese Relation auch die Kleiner-Relation und schreiben \(x<y\), falls \(xRy\).

Example 25

Wir definieren eine weitere Relation \(R\subset \mathbb{R}\times \mathbb{R}\) wie folgt:

\[R=\left\{(x,y)\in \mathbb{R}\times \mathbb{R} \ \vert \ x=y \right\}\]

Wir nennen diese Relation auch die Gleich-Relation und schreiben \(x=y\), falls \(xRy\).

Wir kennen Relationen also schon, ohne es zu wissen. Die Zeichen \(=,\not =, < ,\leq,>,\geq\) sind alle binäre Relationen mit der Grundmenge \(\mathbb{R}\).

Darstellung binärer Relationen

Binäre Relationen lassen sich im Falle von endlichen Mengen \(A_1\) und \(A_2\) kompakt darstellen. Dabei gibt es zwei Möglichkeiten der Darstellung, die wir im Folgenden näher betrachten wollen:

• Pfeildarstellung

• Matrixdarstellung

Hierfür betrachten wir folgendes Beispiel. Sei \(A\) die Menge der Studierenden der THB

• \(A_1=\left\{S_1,\dots, S_n\right\}\)

Sei weiterhin \(A_2\) die Menge der Vorlesungen, die an der THB angeboten werden.

• \(A_2=\left\{ "Grundlagen der Mathematik", "Programmieren 1", "Programmieren 2", ... \right\}\)

Wir wollen nun die Relation “Vorlesungsbelegung SoSE23” beschreiben, welche ausdrückt, welche Studierenden im SoSE23 welche Vorlesung belegt haben.

Pfeildarstellung

Die Pfeildarstellung ist fast selbsterklärend. Wir sehen anhand der Darstellung, dass Student:in \(S_1\) die Fächer “Grundlagen der Mathematik” und “Programmieren 1” belegt hat. Hingegen belegt Student:in \(S_4\) die Fächer “Programmieren 1” und “Programmieren 2” gleichzeitig.

Matrixdarstellung

	\(S_1\)	\(S_2\)	\(S_3\)	\(S_4\)	\(\dots\)	\(S_n\)
“Grundlagen der Mathematik”	x		x
“Programmieren 1”	x	x		x		x
“Programmieren 2”				x
\(\vdots\)

Die Matrixdarstellung ist eine tabellarische Darstellung, bei der wir an jeder Spalten-Zeilen-Kombination ein x schreiben, falls die Kombination in der Relation enthalten ist.

Eigenschaften binärer Relationen

Es gibt viele definierende Eigenschaften von Relationen, die wir hier kurz zusammenfassen wollen. Im Folgenden sei \(R\) immer eine homogene binäre Relation.

Reflexiv

Definition 22

Sei \(R\) eine homogene binäre Relation mit Grundmenge \(A\). Dann nennen wir \(R\) reflexiv, falls

\[xRx \text{ für alle } x\in A\]

In der Sprache der Prädikatenlogik können wir schreiben:

\[\forall x\in A: xRx.\]

Reflexivität bedeutet also, dass \(x\) mit sich selbst in Beziehung stehen muss für alle \(x\in A\).

Frage

Welche der Relationen \(=,\not =, < ,\leq,>,\geq\) sind reflexiv?

Antwort

Die Relationen \(=,\leq,\geq\).

Symmetrisch

Definition 23

Sei \(R\) eine homogene binäre Relation mit Grundmenge \(A\). Dann nennen wir \(R\) symmetrisch, falls für alle \(x,y\in A\) mit \(xRy\) auch gilt \(yRx\).

In der Sprache der Prädikatenlogik können wir schreiben:

\[\forall x,y\in A: (xRy \to yRx).\]

Symmetrie bedeutet also, dass die Relation keine Reihenfolge kennt. Wir können die Reihenfolge von \(x\) und \(y\) beliebig tauschen.

Frage

Welche der Relationen \(=,\not =, < ,\leq,>,\geq\) sind symmetrisch?

Antwort

Die Relationen \(=\) und \(\not =\).

Antisymmetrisch

Definition 24

Sei \(R\) eine homogene binäre Relation mit Grundmenge \(A\). Dann nennen wir \(R\) antisymmetrisch, falls für alle \(x,y\in A\) mit sowohl \(xRy\) als auch \(yRx\) gilt, dass \(x=y\) sein muss.

In der Sprache der Prädikatenlogik können wir schreiben:

\[\forall x,y\in A: ((xRy \land yRx) \to x=y).\]

Antisymmetrie bedeutet also, dass die einzige Möglichkeit, dass \(x\) und \(y\) von beiden Seiten in Relation stehen, darin besteht, dass \(x=y\) sein muss.

Frage

Welche der Relationen \(=,\not =, < ,\leq,>,\geq\) sind antisymmetrisch?

Antwort

Die Relationen \(=, < ,\leq,>,\geq\) sind antisymmetrisch. Für die Relationen \(\leq\) und \(\geq \) ist das einfacher zu sehen. Für die Relationen \(<,>\) liegt das daran, dass niemals \(x<y\) und \(y<x\) gleichzeitig gelten kann. Also ist der linke Teil der Implikation immer falsch.

Übung: Warum ist \(=\) antisymmetrisch?

Transitiv

Definition 25

Sei \(R\) eine homogene binäre Relation mit Grundmenge \(A\). Dann nennen wir \(R\) transitiv, falls für alle \(x,y,z\in A\) mit \(xRy\) und \(yRz\) auch gilt: \(xRz\).

In der Sprache der Prädikatenlogik können wir schreiben:

\[\forall x,y,z\in A: ((xRy \land yRz)\to xRz).\]

Transitivität heißt also, wenn \(x\) in Relation zu \(y\) steht und \(y\) in Relation zu \(z\), dann steht auch \(x\) in Relation zu \(z\).

Frage

Welche der Relationen \(=,\not =, < ,\leq,>,\geq\) sind transitiv?

Antwort

Die Relationen \(=, < ,\leq,>,\geq\) sind alle transitiv. Wir betrachten das Beispiel \(<\). Falls die Zahl \(x<y\) und \(y<z\). Dann haben wir drei Zahlen \(x,y,z\) in aufsteigender Reihenfolge. Es gilt demnach natürlich auch \(x<z\), was genau die Transitivität bedeutet.

3.2.3 Ordnungen

Ordnungsrelationen sind eine Verallgemeinerung der Relationen \(\geq,\leq\), die wir schon für Zahlen kennen. Zunächst einmal definieren wir formal eine Ordnungsrelation und betrachten dann, warum diese Definition sinnvoll ist.

Definition 26

Eine binäre homogene Relation \(R\subset A\times A\) heißt Ordnung, falls \(R\) folgende Eigenschaften besitzt:

• reflexiv

• antisymmetrisch

• transitiv

Example 26

Wir haben bereits anhand der Beispiele gesehen, dass nach obiger Definition \(=,\leq,\geq\) Ordnungen sind.

Example 27

Sei \(A=\mathcal{P}(\mathbb{N})\). Dann definieren wir eine Ordnung \(R\subset \mathcal{P}(\mathbb{N})\times \mathcal{P}(\mathbb{N})\) wie folgt:

\[R=\left\{ (A,B)\in \mathcal{P}(\mathbb{N})\times \mathcal{P}(\mathbb{N}) \ \vert \ A\subset B \right\}\]

Beweis:

• Reflexiv:

Wir müssen zeigen, dass für alle Mengen \(A\in \mathcal{P}(\mathbb{N})\) gilt \((A,A)\in R\). D.h. wir müssen zeigen, dass \(A\subset A\). Das gilt aber trivialerweise.

• Antisymmetrisch:

Sei nun \((A,B) \in R\) und \((B,A)\in R\). D.h. es gilt sowohl \(A\subset B\) als auch \(B\subset A\). Dann ist nach Definition \(A=B\) und das zeigt die Behauptung.

• Transitiv:

Sei nun \((A,B) \in R\) und \((B,C)\in R\). Also \(A\subset B\) und \(B\subset C\). Dann gilt \(A\subset C\) (Übung!).

Definition 27

Sei \(R\subset A\times A\) eine Ordnung. Dann nennen wir \(A\) eine geordnete Menge bzgl. \(A\).

Es ist also \(\mathcal{P}(\mathbb{N})\) eine geordnete Menge bezüglich der obigen Relation “\(\subset\)”. Das heißt aber nicht, dass wir alle Elemente in \(A\) miteinander “vergleichen” können. So kann es zwei Teilmengen \(A,B\subset \mathbb{N}\) geben, für die weder \(A\subset B\) noch \(B\subset A\) gilt. Z.B. \(A=\{1,2,3\}\) und \(B=\{4,5,6,7\}\).

Im Gegensatz dazu ist in \(\mathbb{N}\) bzgl. \(\leq\) jede Zahl vergleichbar, denn für zwei Zahlen \(n,m\in \mathbb{N}\) gilt immer \(a\leq b\) oder \(b\leq a\).

Solch eine Ordnung nennen wir totale Ordnung.

Definition 28

Sei \(A\) eine geordnete Menge bzgl. der Relation \(R\). Dann nennen wir \(R\) eine totale Ordnung, falls für alle \(a,b\in A\) gilt:

\[aRb \quad \text{ oder } bRa.\]

3.2.5 Äquivalenzrelationen (optional)

Eine weitere wichtige binäre Relation ist die Äquivalenzrelation. Die Äquivalenzrelation regelt, welche Objekte wir als identisch miteinander setzen wollen. So gibt es beispielsweise in der Zahlentheorie manchmal Situationen, in denen wir alle Zahlen, die gerade sind, als identisch setzen wollen und nur den Unterschied machen wollen zwischen gerade und ungerade. Oder wir wollen nur den Rest durch 3 oder durch 7 oder eine beliebige Zahl \(n\) unterscheiden. Hierfür eignen sich die sogenannten Äquivalenzrelationen, wie wir gleich sehen werden.

Aber erstmal wollen wir die Äquivalenzrelation formal einführen.

Definition 29

Eine binäre homogene Relation \(R\subset A\times A\) heißt Äquivalenzrelation, falls \(R\) folgende Eigenschaften besitzt:

• reflexiv

• symmetrisch

• transitiv

Example 28

Von den Relationen \(=,\not =, < ,\leq,>,\geq\) ist nur \(=\) eine Äquivalenzrelation, denn alle anderen sind nicht symmetrisch.

Example 29

Sei nun \(A=\mathbb{N}\) und wir definieren folgende Relation \(R\subset \mathbb{Z}\times \mathbb{Z}\).

\[R=\{(a,b)\in \mathbb{Z}\times \mathbb{Z} \ \vert \ a-b \text{ ist durch 3 teilbar}\}\]

Beweis:

• Reflexiv

Es gilt für alle \(n\in \mathbb{Z}\), dass \(n-n=0\). Die Zahl \(0\) ist durch alle Zahlen teilbar. Insbesondere durch 3.

• Symmetrisch

Sei \(a,b \in \mathbb{Z}\) mit \(aRb\), d.h. \(a-b\) ist durch drei teilbar. Wir müssen zeigen, dass \(b-a\) durch 3 teilbar ist. Es gilt jedoch \(b-a=-(a-b)\) und da jede negative einer durch 3 teilbaren Zahl wieder durch 3 teilbar ist, gilt damit die Behauptung.

• Transitiv

Sei nun \(a,b,c\in \mathbb{Z}\) mit \(a-b\) und \(b-c\) durch drei teilbar. Die Summe zweier Zahlen, die durch 3 teilbar ist, ist wieder durch drei teilbar. Damit ist

\[(a-b)+(b-c)=a-c\]

durch drei teilbar. Also \(aRc\).

Wir haben also gesehen, dass \(R\) eine Äquivalenzrelation ist. Die Zahl \(3\) hat hierbei keine Rolle gespielt und wir hätten alle Zahlen einsetzen können. Wir schreiben, falls \(aRb\) gilt, auch \(a\equiv_3 b\) oder \(a=b \mod 3\).

Wir haben also gesehen, wie wir Äquivalenzrelationen nutzen können, um mit “Resten” zu rechnen.

Eine weitere wichtige Eigenschaft von Äquivalenzrelationen ist, dass sie eine Aufteilung der Menge \(A\) in sogenannte Äquivalenzklassen induzieren.

Definition 30

Sei \(R\subset A\times A\) eine Äquivalenzrelation. Sei \(x\in A\). Dann nennt man

\[[x]_R =\left\{ y\in A \ \vert \ xRy \right\}\]

eine Äquivalenzklasse von \(A\). Das Element \(x\) heißt Repräsentant der Äquivalenzklasse und die Anzahl der Äquivalenzklassen heißt Index.

Example 30

Die Äquivalenzklassen der Relation \(\equiv_3\) sind gegeben durch:

• \([0]_3= \{\dots, -3,0,3,6,\dots\}\)

• \([1]_3= \{\dots, -2,1,4,7,\dots\}\)

• \([2]_3=\{ -1,2,5,8,\dots\}\)

Wie wir sehen, gibt es also drei disjunkte Äquivalenzklassen, deren Vereinigung die ganzen Zahlen bildet.

Wir nennen in diesem Fall die Äquivalenzklassen auch Restklassen.

Tatsächlich sind obige Beobachtungen kein Spezialfall. Es gilt der folgende Satz.

Theorem 16

Sei \(R\subset A\times A\) eine Äquivalenzrelation. Dann gilt:

1. \([y]_R=[x]_R \) für alle \(y\in [x]_R\)

2. Für \(x,y\in A\) mit \((x,y)\not\in R\) gilt \([x]_R\cap [y]_R =\emptyset\)

3. Es gilt

\[A= \bigcup_{x\in A} [x]_R.\]

D.h. die Äquivalenzklassen bilden eine Überdeckung.

3.3 Funktionen

Funktionen bilden eine der wichtigsten Klassen von Relationen.

Die charakteristische Eigenschaft von Funktionen ist, dass, im Gegensatz zu allgemeinen Relationen, jedem Wert aus einer Definitionsmenge \(X\) genau ein Wert aus der Zielmenge zugeordnet wird.

Als Beispiel dient die Zuordnung von Studiengängen zu Studierenden:

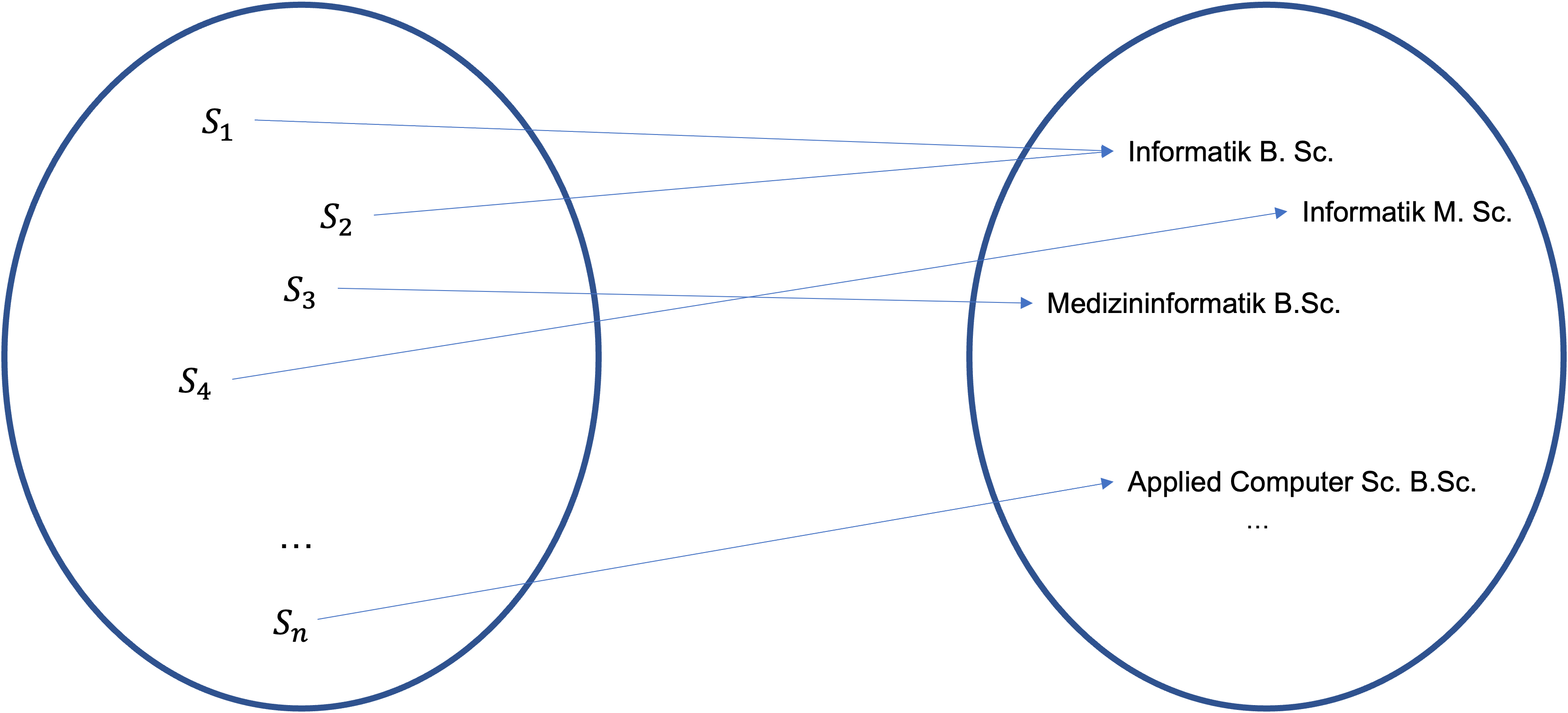
Wichtig ist hierbei zu bemerken, dass ein:e Student:in genau einem Studiengang zugeordnet werden kann. Es können zwar mehrere Studierende dem gleichen Studiengang zugeordnet werden, aber eben nicht ein:e Student:in mehreren Studiengängen.

3.3.1 Definition einer Funktion

Definition 31

Es seien \(X\) und \(Y\) beliebige Mengen. Eine Funktion \(f\) ordnet jedem Element \(x\in X\) genau ein Element \(y\in Y\) zu.

Wir schreiben

\[\begin{split}f\colon X\to Y\\ x\mapsto f(x).\end{split}\]

Wir schreiben auch \(f(x)\in Y\) für den Wert, der (unter \(f\)) dem Wert \(y\) zugeordnet wird. Die Menge \(X\) nennen wir dann Definitionsmenge und die Menge \(Y\) nennen wir Zielmenge.

Example 31

• Die Funktion

\[\begin{split}f\colon \mathbb{R}\to \mathbb{R}\\ x\mapsto x^2\end{split}\]

kennen Sie vermutlich noch aus der Schule.

• Die Funktion

\[\begin{split}f\colon \mathbb{R}\setminus\{0\}\to \mathbb{R}\\ x\mapsto \frac{1}{x}\end{split}\]

ist ebenfalls definiert. Hierbei ist es jedoch essentiell, dass wir in der Definitionsmenge die \(0\) entfernt haben. Andererseits würde es sich nicht um eine Funktion handeln, da wir die \(0\) nicht zuordnen können.

Folgende Beispiele sind keine Funktion:

• Wenn wir das erste Beispiel leicht modifizieren, erhalten wir keine gültige Funktion:

\[\begin{split}f\colon \mathbb{R}\to (0,\infty)\\ x\mapsto x^2.\end{split}\]

Dies ist keine gültige Funktion, da \(0\) auf \(0\) abgebildet werden würde, aber \(0\not \in (0,\infty)\), also nicht in der Zielmenge liegt.

• Das zweite Beispiel ist auch keine Funktion, wenn wir die \(0\) nicht ausschließen:

\[\begin{split}f\colon \mathbb{R}\to \mathbb{R}\\ x\mapsto \frac{1}{x}.\end{split}\]

Definition 32

Sei \(f\colon X\to Y\) eine Funktion mit \(x\mapsto f(x)\). Dann nennen wir die Menge

\[f(X)=\{f(x)\in Y \ \vert \ x\in X\}\]

das Bild von \(X\) unter \(f\). Manchmal nennen wir \(f(X)\) auch den Wertebereich von \(f\).

Example 32

• Betrachten wir die Funktion

\[\begin{split}f\colon \mathbb{R}\to \mathbb{R}\\ x\mapsto x^2.\end{split}\]

Dann gilt

\[f(X)=[0,\infty).\]

• Betrachten wir nun die Funktion

\[\begin{split}f\colon \mathbb{R}\setminus\{0\}\to \mathbb{R}\\ x\mapsto \frac{1}{x}.\end{split}\]

Dann gilt:

\[f(X)=\mathbb{R}\setminus\{0\}\]

3.3.2 Funktionen als Relationen

Was haben nun Funktionen mit Relationen zu tun? Auf den ersten Blick scheinen es komplett verschiedene Definitionen zu sein.

Wir können aber wie folgt eine Funktion als Relation verstehen.

Sei dazu \(f\) eine Funktion

\[\begin{split}f\colon X\to Y\\ x\mapsto f(x).\end{split}\]

Wir können nun folgende Menge definieren:

\[\{(x,f(x))\in X\times Y \ \vert x\in X\} \subset X\times Y.\]

Wie wir sehen, können wir also mithilfe der Funktion eine binäre Relation definieren.

Frage: Gilt auch das umgekehrt? Also ist jede Relation auch eine Funktion?

Antwort:

Nein. Denn es ist nicht sichergestellt, dass dann jedem \(x\in X\) genau ein \(y\) zugeordnet wird.

Hierfür brauchen wir eine zusätzliche Definition.

Definition 33

Eine binäre Relation \(R\subset X\times Y\) heißt rechtseindeutig, falls für alle \(x_1Ry_1\) und \(x_2Ry_2\) mit \(x_1=x_2\) auch gilt \(y_1=y_2\).

Damit können wir nun sagen:

Eine Funktion ist eine rechtseindeutige binäre Relation.

Example 33

Gegeben sei folgende Relation \(R=\{(1,2),(3,4),(1,8),(2,7)\}\subset \mathbb{N}\times \mathbb{N}\).

Ist diese Funktion rechtseindeutig?

Nein, denn wir haben die beiden Elemente \((1,2)\) und \((1,8)\). D.h. zwei Elemente, von denen die linke Seite identisch ist, aber die rechte Seite verschieden. Es ist also keine rechtseindeutige Relation und stellt somit auch keine Funktion dar.

3.3.3 Darstellung von Funktionen

Es gibt in der Sprache der Mathematik mehrere Möglichkeiten, eine Funktion zu definieren.

Eine haben Sie schon gesehen, indem wir eine Formel angeben wie beispielsweise \(x^2\) oder \(1/x\).

Wir wollen in diesem Abschnitt zwei weitere Möglichkeiten vorstellen.

Wertetabelle

Wie wir gesehen haben, ist eine Funktion nichts anderes als eine rechtseindeutige Relation. Wenn wir es mit endlichen Mengen \(X\) und \(Y\) zu tun haben, reicht es auch zusätzlich zu den Mengen \(X\) und \(Y\) die Relation \(R\) in aufzählender Form anzugeben. Dies kann am anschaulichsten über eine Tabelle gemacht werden.

Machen wir ein Beispiel.

Sei \(X=\{0,1,2,3,4\}\) und \(Y=\{5,6,7,8\}\). Dann können wir die Relation einfach aufzählen. Z.B.

\[\{(0,8),(1,7),(2,8),(3,5),(4,8)\}\subset X\times Y.\]

Dies können wir wie erwähnt auch in einer Tabellenform angeben.

\(x\):	0	1	2	3	4
\(f(x)\):	8	7	8	5	8

Solch eine Tabelle nennen wir Wertetabelle.

Wichtig Eine Wertetabelle alleine ist noch keine Funktion. Es muss noch die Zielmenge \(Y\) angegeben werden, um eine Funktion zu definieren.

Abschnittsweise definierte Funktionen

Manche Funktionsvorschriften lassen sich nicht für alle Werte aus einer Definitionsmenge mit einem einzigen Ausdruck definieren. In diesem Fall können wir die Funktion auch abschnittsweise definieren.

Als Beispiel wollen wir die Betragsfunktion für eine reelle Zahl heranziehen. Der Betrag einer Zahl \(x\in\mathbb{R}\) ist dabei definiert als der “Abstand” zum Nullpunkt und wird mit \(\vert x\vert\) beschrieben. Zum Beispiel ist \(\vert 3 \vert =3\) und \(\vert -4,5\vert =4,5\).

Es handelt sich also um eine Funktion:

\[\vert \cdot \vert \colon \mathbb{R}\to \mathbb{R}.\]

Für \(x\geq 0\), können wir \(\vert x \vert =x\) definieren. Falls nun \(x\) negativ ist, so bekommen wir mit \(-x\) wieder eine positive Zahl. Also ist für \(x<0\) der Betrag durch \(\vert x \vert =-x \) definiert.

Wir schreiben dann

\[\begin{split}\vert \cdot \vert \colon \mathbb{R}&\to \mathbb{R}\\ x&\mapsto \begin{cases} x & x\geq 0 \\ -x & x<0 \end{cases}\end{split}\]

3.3.4 Verknüpfung von Funktionen

Wir können Funktionen miteinander verknüpfen. Nehmen wir an, wir haben unsere obige Funktion, die Studierenden Fachbereiche zuordnet. Nehmen wir nun an, wir haben eine weitere Funktion, die den Fachbereichen eine Regelstudienzeit zuordnet.

Dann können wir beide Funktionen miteinander verknüpfen und können damit Studierenden eine Regelstudienzeit zuordnen.

Definition 34

Sei \(f\colon A\to B\) und \(g\colon C\to D\) zwei Funktionen mit \(f(A)\subset C\). Dann definieren wir die verknüpfte Funktion \(g\circ f\) wie folgt:

\[\begin{split}(g\circ f) \colon X\to Z\\ x\mapsto g(f(x)).\end{split}\]

Wichtig

• Bei der Verknüpfung \(g\circ f\) wird zuerst \(f\) ausgeführt und dann erst \(g\). Das mag am Anfang etwas unintuitiv wirken, da wir von rechts nach links lesen.

• Damit wir \(g\circ f\) definieren können, muss \(f(A)\subset C\) sein, denn ansonsten ist \(g(f(x))\) nicht definiert.

Example 34

Sei \(f\colon \mathbb{R}\setminus \{0\} \to \mathbb{R}, \quad x \mapsto \frac{1}{x}\) und \(g\colon \mathbb{R} \to \mathbb{R}, \quad x \mapsto x^2\). Dann ist

\[\begin{split}(g\circ f) \colon \mathbb{R}\setminus \{0\}\to \mathbb{R}\setminus \{0\}\\ x\mapsto \frac{1}{x^2}.\end{split}\]

Die Funktion \(f\circ g\) kann nicht definiert werden, denn \(f(\mathbb{R})\not \subset\mathbb{R}\setminus \{0\}\). (Übung: Warum?)

3.3.5 Die Umkehrfunktion

Nehmen wir an, wir haben eine Funktion \(f\colon S\to M\), die jedem Studierenden eine Matrikelnummer zuordnet, wobei \(S\) die Menge der Studierenden und \(M\) die Menge aller vergebenen Matrikelnummern bezeichnet.

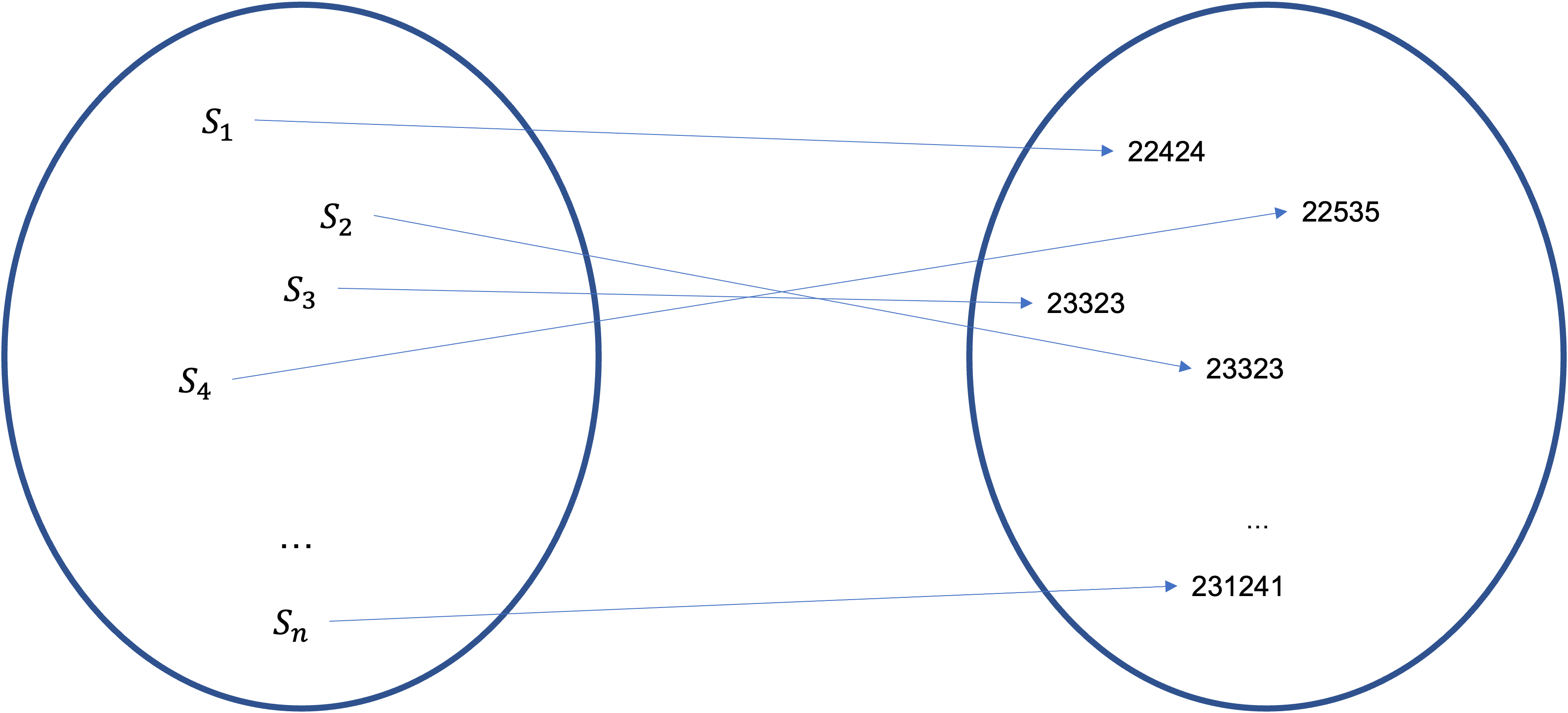
Nehmen wir nun an, wir kennen eine Matrikelnummer und wir wollen wissen, zu welchem Studierenden diese gehört. Im Prinzip sollte das möglich sein, denn die Beziehung ist eine 1:1-Beziehung.

Wir suchen also die Umkehrfunktion

\[f^{-1}\colon M\to S.\]

Sei nun \(Pauline\) eine Studentin mit Matrikelnummer 123. Dann gilt \(f(Pauline)=123\) und \(f^{-1}(123)=Pauline\).

Es gilt also:

\[\begin{split}(f^{-1}\circ f)(Pauline)=Pauline \text{ und }\\ (f\circ f^{-1})(123)=123.\end{split}\]

Wir nennen dann \(f^{-1}\) die Umkehrfunktion von \(f\).

Definition 35

Sei \(f\colon X\to Y\) eine Funktion. Dann nennen wir \(f^{-1}\colon Y\to X\) die Umkehrfunktion von \(f\), falls gilt:

\[\begin{split}f^{-1}(f(x))=x \text{ für alle } x\in X \text{ und}\\ f(f^{-1}(y))=y \text{ für alle }y\in Y.\end{split}\]

Example 35

Sei \(f\colon \mathbb{R}\to \mathbb{R} \quad x\mapsto 2x+1\).

Dann ist \(f^{-1}\colon \mathbb{R}\to \mathbb{R} \quad x\mapsto 0,5x-0,5\).

Denn es gilt:

\[\begin{split}f^{-1}(f(x))=f^{-1}(2x+1)=0.5(2x+1)-0,5=x \text{ und }\\ f(f^{-1}(x))=f(0.5x-1)=2(0,5x-0,5)+1=x.\end{split}\]

Es stellt sich die Frage, wann eine Funktion eine Umkehrfunktion besitzt. Wir haben bereits erwähnt, dass es sich wohl um eine 1:1-Beziehung handeln muss.

Das können wir noch etwas genauer aufsplitten, nämlich in die Injektivität und Surjektivität einer Funktion.

Injektivität

Injektive Funktionen sind eindeutige Funktionen. Es kann also nicht vorkommen, dass zwei Elemente auf dasselbe Element abgebildet werden. Das gilt insbesondere bei unserer Funktion, die Studierenden eine Matrikelnummer zuweist. Denn ansonsten könnte man die Studierenden nicht eindeutig durch Angabe der Matrikelnummer unterscheiden.

Definition 36

Sei \(f\colon X\to Y\) eine Funktion. Wir nennen \(f\) injektiv, falls für alle \(x_1,x_2\in X\) mit \(f(x_1)=f(x_2)\) gilt \(x_1=x_2\).

Wenn wir die Funktion \(f\) mithilfe eines Pfeildiagramms beschreiben, bedeutet injektiv, dass auf jedes Element der Zielmenge \(Y\) maximal ein Pfeil zeigt.

Umgekehrt ist eine Funktion nicht injektiv, falls es mindestens ein Element gibt, auf das mindestens zwei Pfeile zeigen.

Example 36

Wir wollen zeigen, dass die Funktion

\[\begin{split}f\colon \mathbb{R}\to \mathbb{R}\\ x\mapsto 3x+1\end{split}\]

injektiv ist.

Seien dazu also \(x_1,x_2\in \mathbb{R}\) mit \(f(x_1)=f(x_2)\). Dann müssen wir zeigen, dass \(x_1=x_2\).

Es gilt also

\[3x_1+1=3x_2+1 \Leftrightarrow 3x_1=3x_2 \Leftrightarrow x_1=x_2.\]

Damit folgt, dass \(x_1=x_2\) und wir haben die Behauptung gezeigt.

Surjektivität

Die zweite wichtige Voraussetzung für die Existenz einer Umkehrfunktion ist die Surjektivität. Während die Injektivität darauf abzielt, dass Matrikelnummern eindeutig sind, zielt die Surjektivität darauf ab, dass die Matrikelnummer überhaupt vergeben ist. Also dass es mindestens einen Studierenden gibt, der dieser Matrikelnummer zugeordnet ist.

Definition 37

Sei \(f\colon X\to Y\) eine Funktion. Wir nennen \(f\) surjektiv, falls für alle \(y\in Y\) ein \(x\in X\) existiert mit \(f(x)=y\).

Wenn wir wieder die Pfeildiagramme betrachten, so bedeutet surjektiv, dass bei jedem \(y\in Y\) mindestens ein Pfeil endet.

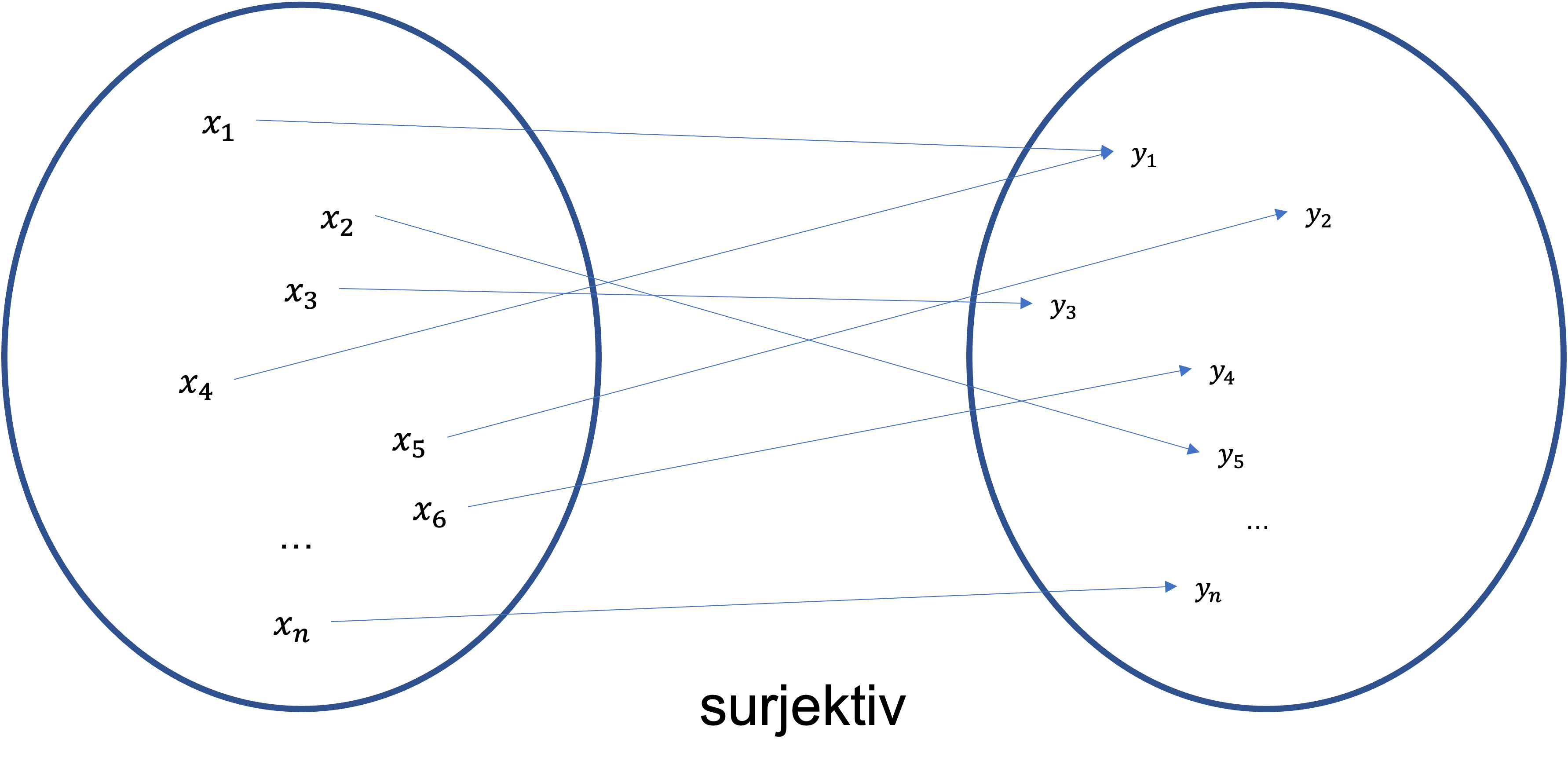
Nicht surjektiv bedeutet dann, dass bei mindestens einem \(y\in Y\) kein Pfeil endet.

Example 37

Wir wollen zeigen, dass die Funktion

\[\begin{split}f\colon \mathbb{R}\to \mathbb{R}\\ x\mapsto 3x+1\end{split}\]

surjektiv ist.

Sei dafür \(y\in Y\) ein beliebiges Element.

Dann wähle \(x=\frac{1}{3}y-\frac{1}{3}\).

Es gilt dann:

\[f(x)=3(\frac{1}{3}y-\frac{1}{3})+1=y\]

Also haben wir für ein beliebiges Element \(y\) ein \(x\) gefunden mit \(f(x)=y\). Damit ist \(f\) surjektiv.

Bijektivität

Beide Eigenschaften, Injektivität und Surjektivität, werden benötigt, um eine Umkehrfunktion zu definieren. Daher geben wir Funktionen mit diesen beiden Eigenschaften einen besonderen Namen.

Definition 38

Eine Funktion \(f\colon X\to Y\) heißt bijektiv, falls sie sowohl injektiv als auch surjektiv ist.

Es gilt nun der folgende Zusammenhang zwischen bijektiven Funktionen und der Umkehrfunktion.

Theorem 17

Sei \(f\colon X\to Y\) eine bijektive Funktion. Dann gibt es die Umkehrfunktion \(f^{-1}\colon Y\to X\).

Example 38

Wir haben bereits gesehen, dass die Funktion

\[\begin{split}f\colon \mathbb{R}\to \mathbb{R}\\ x\mapsto 3x+1\end{split}\]

injektiv und surjektiv ist. Sie ist also bijektiv und damit besitzt sie eine Umkehrfunktion.