Kapitel 6 – Lineare Transformationen in der Ebene#

6.1 Lernziele#

In diesem Abschnitt wollen wir lineare Transformationen in der Ebene mittels Matrizen genauer untersuchen.

Lernziele

  • Zusammenhang zwischen einer \(2\times 2\)-Matrix und einer geometrischen Transformation

  • Skalierungsmatrizen interpretieren und anwenden

  • Spiegelung als Matrixtransformation interpretieren und anwenden

  • Rotation als Matrixtransformation interpretieren und anwenden

  • Praxisbeispiel für die Bildbearbeitung in Python kennenlernen

6.2 Einführung#

Wir konzentrieren uns in diesem Kapitel vor allem auf den \(\mathbb{R}^2\), d. h. wir betrachten Transformationen in der Ebene.

Wir zeigen zunächst, wie wir Matrizen \(A\in \mathbb{R}^{2\times 2}\) als geometrische Transformationen interpretieren können.

Dies geschieht durch folgende Interpretation von Matrizen als Abbildungen.

Definition 48

Sei \(A\in \mathbb{R}^{m\times n}\), so ist die lineare Transformation von \(A\) definiert als die folgende Funktion

\[T_A\colon \mathbb{R}^n \to \mathbb{R}^m \quad v\mapsto A\cdot v.\]

Wir nennen die Matrix \(A\) zu der linearen Transformation \(T_A\) die Abbildungsmatrix.

Falls \(A\in \mathbb{R}^{2\times 2}\), so nennen wir die entsprechende lineare Transformation eine lineare Transformation in der Ebene.

Remark 3

Obige Definition ist wohldefiniert. Dafür betrachten wir einmal kurz die Dimensionen.

Wenn \(A\in \mathbb{R}^{m\times n}\) und \(v\in \mathbb{R}^n=\mathbb{R}^{n\times 1}\), so gilt nach der Dimensionsformel (\((m\times n)\cdot (n\times 1)\)), dass das Ergebnis die Dimension \((m\times 1)\) besitzt, also ein \(m\)-dimensionaler Spaltenvektor.

Für \(A\in \mathbb{R}^{2\times 2}\) bedeutet dies, dass wir einen 2-dimensionalen Vektor auf einen 2-dimensionalen Vektor abbilden.

Lineare Transformationen (der Ebene) haben die folgende, für Linearität charakteristische Eigenschaft.

Theorem 21

Sei \(A\in\mathbb{R}^{2\times 2}\) eine Matrix und \(T_A\) die zugehörige lineare Transformation.

  • Der Nullvektor wird wieder auf den Nullvektor abgebildet.

  • Geraden werden wieder auf Geraden abgebildet.

  • Parallele Geraden bleiben parallel.

Example 53

Nach obigem Satz sehen wir, dass die Translation/Verschiebung eines Objektes keine lineare Transformation darstellt, da der Nullvektor nicht wieder auf den Nullvektor abgebildet wird.

Wir werden jedoch sehen, dass die folgenden Transformationen lineare Transformationen darstellen:

  • Spiegelung

  • Skalierung

  • Rotation

Example 54

Sei \(A=\begin{pmatrix}1 & 2 \\ 2 & 1\end{pmatrix}\).

Um die lineare Transformation genauer zu verstehen, ist es häufig hilfreich, sich zu visualisieren, wie die Basisvektoren \(e_1=\begin{pmatrix}1\\0\end{pmatrix}\) und \(e_2=\begin{pmatrix}0\\1\end{pmatrix}\) transformiert werden. Wie man leicht nachrechnet, werden diese auf die Vektoren \(Ae_1=\begin{pmatrix}1\\2\end{pmatrix}\) und \(Ae_2=\begin{pmatrix}2\\1\end{pmatrix}\) abgebildet.

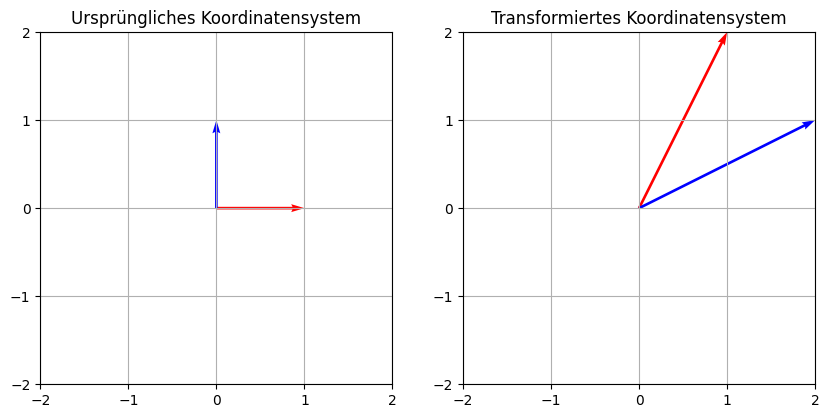
Wir können nun auch betrachten, was passiert, wenn wir die Punkte eines Dreiecks transformieren: .

Wir sehen, dass das Dreieck wieder ein Dreieck ist, aber sich Längen und Winkel unterscheiden. Wir sehen auch, dass beide Dreiecke den Nullpunkt beinhalten.

6.3 Skalierung als lineare Transformation#

Skalierung bedeutet Strecken und Stauchen von geometrischen Objekten.

Mittels der skalaren Multiplikation mit einem positiven \(\lambda>0\) erhalten wir über \(v\mapsto \lambda v\) eine einfache mathematische Beschreibung von Streckung und Stauchung: Es ist eine Streckung, falls \(\lambda>1\), und eine Stauchung, falls \(\lambda<1\).

In Matrixform können wir dies auch so schreiben:

\[\begin{split}S(\lambda,\lambda)=\begin{pmatrix}\lambda & 0 \\ 0 & \lambda\end{pmatrix}.\end{split}\]

Wollen wir in \(x\)- und \(y\)-Richtung mit verschiedenen Streckungsfaktoren arbeiten, so verwenden wir allgemein

\[\begin{split}S(\lambda,\mu)=\begin{pmatrix} \lambda & 0 \\ 0 & \mu \end{pmatrix} \text { für } \lambda, \mu>0.\end{split}\]

Machen wir wieder ein Beispiel:

Example 55

Wir betrachten nun die Matrix

\[\begin{split}S(2,3)= \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}.\end{split}\]

Wieder betrachten wir zunächst die transformierten Basisvektoren

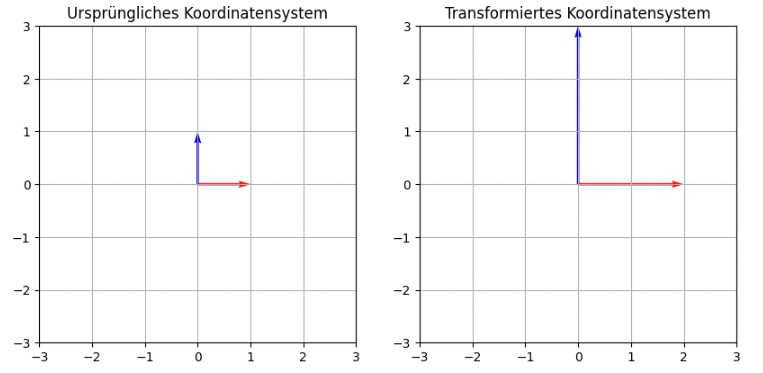
Und nun ein transformiertes Dreieck

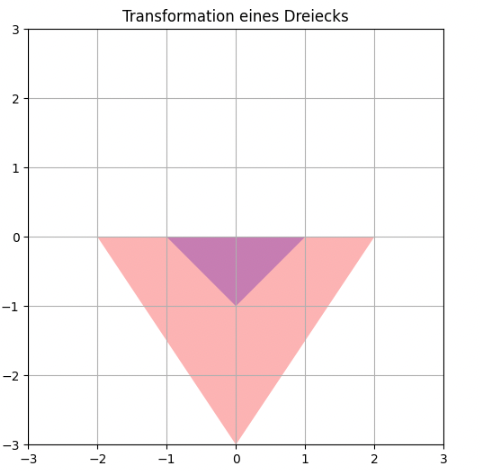
Wir sehen, dass sich die Grundlinie des Dreiecks verdoppelt und die Höhe verdreifacht.

6.4 Spiegelung als lineare Transformation#

Spiegelungen lassen sich ebenfalls als lineare Transformationen darstellen. In der Ebene gibt es drei grundlegende Fälle:

  • Punktspiegelung

  • Spiegelung an der \(y\)-Achse

  • Spiegelung an der \(x\)-Achse

Ähnlich wie bei Streckungen lassen sich die Matrizen durch Diagonalmatrizen darstellen; diesmal erlauben wir auch negative Zahlen.

Hier ist der Überblick über die Spiegelung:

Matrix

geom. Bedeutung

S(-1, 1)

\(\begin{pmatrix}-1 & 0 \\ 0 & 1\end{pmatrix}\)

Spiegelung an der \(y\)-Achse

S(1, -1)

\(\begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\)

Spiegelung an der \(x\)-Achse

S(-1, -1)

\(\begin{pmatrix}-1 & 0 \\ 0 & -1\end{pmatrix}\)

Punktspiegelung am Ursprung

Example 56

Wir betrachten nun die Matrix

\[\begin{split}S(-1,1)= \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}.\end{split}\]

Also die Spiegelung an der \(y\)-Achse. Wieder betrachten wir zunächst die transformierten Basisvektoren

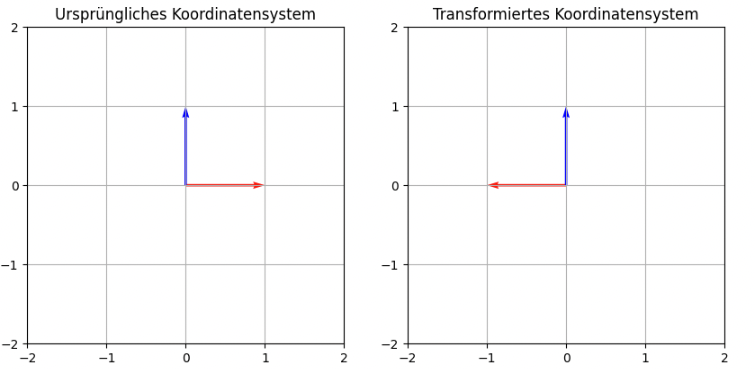
Und nun ein transformiertes Dreieck

Wir sehen, dass das transformierte Dreieck mit dem ursprünglichen identisch ist, da es achsensymmetrisch zur \(y\)-Achse ist.

Wir können zum Beispiel den unteren Punkt nehmen und dies nachvollziehen:

\[\begin{split}\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 0 \\ -1 \end{pmatrix}=\begin{pmatrix} 0 \\ -1 \end{pmatrix}.\end{split}\]

D. h. der Punkt bleibt, wo er ist.

Es kann nun leicht nachgerechnet werden, dass die beiden anderen Punkte ihre Positionen tauschen.

6.5 Rotation als lineare Transformation#

Die Rotation ist die komplizierteste Variante der linearen Transformation. Dabei stellt sich zunächst die Frage, in welche Richtung und um welchen Winkel rotiert wird. Mathematisch bezeichnet die positive Richtung immer die Drehung gegen den Uhrzeigersinn. Wenn wir also von einer Drehung um \(90^\circ\) sprechen, meinen wir eine Drehung um \(90^\circ\) gegen den Uhrzeigersinn.

Wir betrachten zunächst ein Beispiel.

Example 57

Wir wollen die \(90^\circ\)-Drehung als Matrix darstellen. Dafür müssen wir überlegen, auf welche Vektoren die Basisvektoren \(e_1\) und \(e_2\) abgebildet werden. \(e_1\) wird auf \(\begin{pmatrix}0\\1\end{pmatrix}\) und \(e_2\) auf \(\begin{pmatrix}0\\-1\end{pmatrix}\) abgebildet.

Damit ergibt sich folgende Matrix:

\[\begin{split}A=\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}.\end{split}\]

Und es ergeben sich folgende Bilder:

Und nun ein transformiertes Dreieck .

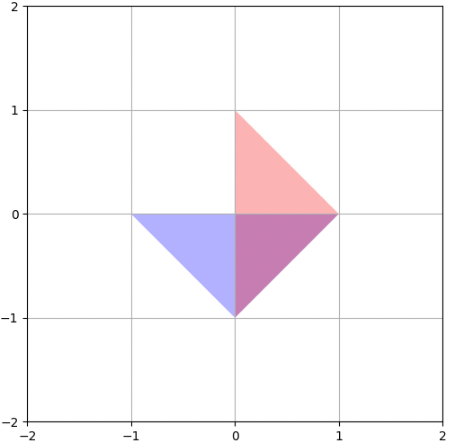Wir haben nun die Rotation für \(90^\circ\) gesehen. Doch wie lautet die allgemeine Formel?

Diese fassen wir im folgenden Satz zusammen.

Theorem 22

Der Ausdruck \(R(\varphi)\) bezeichnet eine Rotation um den Winkel \(\varphi\) mit dem Ursprung als Rotationszentrum. Sie lässt sich durch folgende Matrix darstellen.

\[\begin{split}R(\varphi)=\begin{pmatrix} \cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \end{pmatrix}.\end{split}\]

Hier ist eine Tabelle mit den wichtigsten Rotationsmatrizen:

Winkel (\(\theta\))

Rotationsmatrix (\(R(\theta)\))

geom. Bedeutung

\(0^\circ\)

\(\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\)

Keine Rotation (Identitätsmatrix)

\(90^\circ\)

\(\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\)

Rotation um \(90^\circ\)

\(180^\circ\)

\(\begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}\)

Rotation um \(180^\circ\)

\(270^\circ\)

\(\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}\)

Rotation um \(270^\circ\)

6.6 Hintereinanderschaltung von linearen Transformationen#

Angenommen, wir wollen eine Kombination aus den obigen linearen Transformationen bilden. Dann stellt sich die Frage, wie wir die zugehörige Matrix erhalten – wollen wir zum Beispiel zuerst rotieren und dann skalieren.

Der folgende Satz liefert dafür die entsprechende Antwort.

Theorem 23

Seien \(A,B\in \mathbb{R}^{2\times2}\). Seien \(T_A\) und \(T_B\) die entsprechenden linearen Transformationen. Sei weiter \(A\cdot B\) das Produkt der beiden Matrizen und \(T_{A\cdot B}\) die entsprechende lineare Transformation. Dann gilt:

\[T_A\circ T_B = T_{AB}.\]

Anders ausgedrückt: Die Hintereinanderausführung zweier linearer Transformationen entspricht auf der Ebene der Matrizen der Matrixmultiplikation.

Auch hierfür wollen wir ein Beispiel betrachten:

Example 58

Wir wollen in diesem Beispiel zunächst um \(90^\circ\) drehen und dann an der \(y\)-Achse spiegeln. Die entsprechende Matrix ist dann laut obigem Satz:

\[\begin{split}S(-1,1)\cdot R(90^\circ) = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}.\end{split}\]

Beachte auch hier, dass wir von rechts nach links lesen. Rechts steht die Rotation, weil wir diese als erste ausführen.

Schauen wir uns nun die entsprechenden Bilder an:

Zunächst die Transformation auf den Basisvektoren:

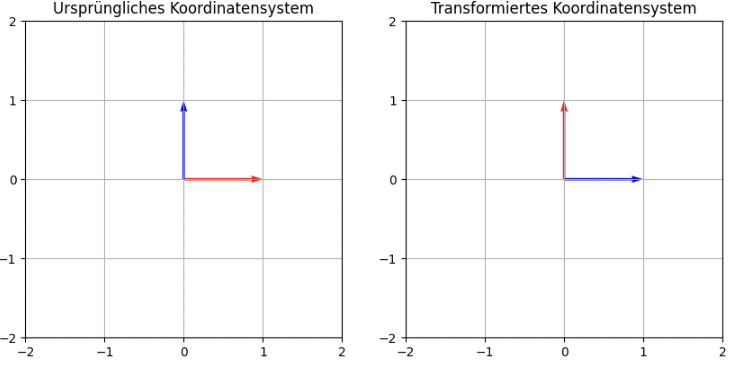
Und nun auf unser Standard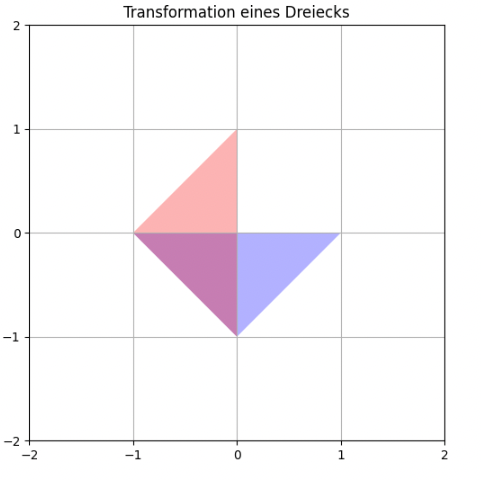dreieck: Auf den ersten Blick sieht das so aus wie eine Drehung um \(90^\circ\) in mathematisch negativer Richtung (Uhrzeigersinn). Dies liegt an der Symmetrie des Dreiecks. Betrachten wir ein weiteres Dreieck: 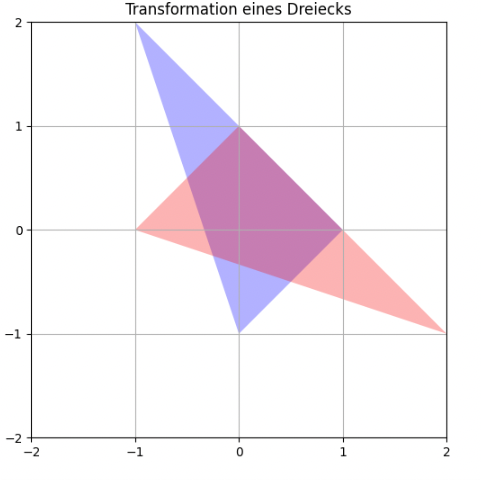Hier sehen wir, dass es keine Rotation ist.

Sehen Sie, wie man die Transformation geometrisch zusammenfassen kann? Antwort:

Es ist die Spiegelung an der Winkelhalbierenden des ersten Quadranten, also an der Geraden \(y=x\).

6.7 Anwendung zur Bearbeitung von Bildern#

Wir wollen unsere neuen Fertigkeiten nun nutzen, um Bilder zu spiegeln, zu rotieren oder zu skalieren. Betrachten Sie dafür folgendes Video.