Kapitel 4 - Der Gauß-Algorithmus

4.1 Lernziele

In diesem Abschnitt lernen wir die folgenden Dinge:

• Grundbegriffe für Lineare Gleichungssysteme

• Den Gauß-Algorithmus

• Anwendung des Page-Rank Algorithmus

• Allgemeine Beschreibung der Lösungsmenge für ein Lineares Gleichungssystem

Lernziele

• Lösen von linearen Gleichungssystemen mittels Gauß-Algorithmus

• Matrizen in Zeilenstufenform bringen

• Geometrisches Verständnis für Lineare Gleichungssysteme

• Zusammenhang herstellen zwischen Lösen von Linearen Gleichungssystemen und dem Pagerank Algorithmus

4.2 Der PageRank Algorithmus als Beispiel

Der PageRank Algorithmus ist ein Verfahren, das von Google entwickelt wurde um die Popularität von Webseiten zu bemessen und damit bessere Suchergebnisse zu produzieren.

Die Grundidee besteht darin, dass wir die Popularität davon abhängt wie viele andere populäre Webseiten auf die ursprüngliche Seite verlinken. Wenn eine Seite also von vielen populären Webseiten verlinkt wird, so ist der PageRank eher groß. Falls es nur von wenigen weniger populären Seiten verlinkt wird so ist er eher klein.

Als Beispiel nehmen wir an, wir haben ein Netzwerk aus vier Webseiten (A,B,C,D). Diese sind wie folgt verlinkt.

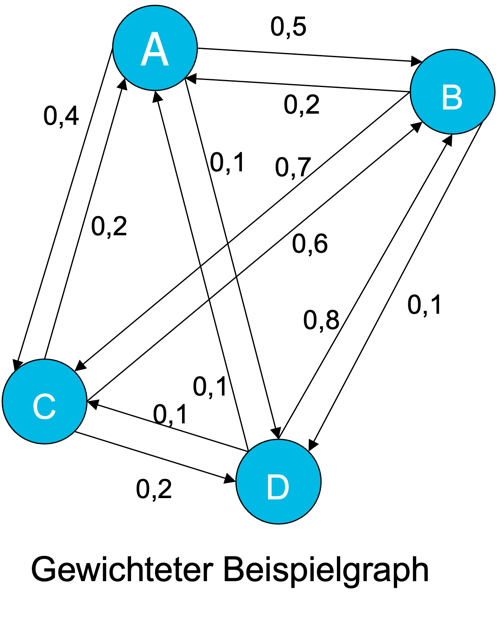
Das heißt, das z.B. 0,5 der Links von Seite A auf Seite B verweisen und 0,2 der Links von B auf A verweisen.

Der Pagerank ist nun durch die folgende Wahrscheinlichkeit gegeben:

\(P(X)\) bezeichnet die Wahrscheinlichkeit, dass ein User sich auf Webseite \(X\) zu einem gegebenen Zeitpunk \(t\) aufhält.

Der Pagerank ist nun die Sortierung nach \(P(X)\). Je größer \(P(X)\) desto populärer ist diese Webseite.

Es gibt nun zwei Möglichkeiten auf die Seite \(X\) zu gelangen:

2 Möglichkeiten

1. User ist auf Webseite Y und klickt auf den Link zu X.

2. User wählt eine zufällige Webseite adhoc aus.

Der Dampingfaktor d (normalerweise gilt d=0,85) besagt, dass mit Wahrscheinlichkeit \(d\) die Möglichkeit 1) passiert und mit Wahrscheinlichkeit \(1-d\) Möglichkeit 2).

Frage: Wie berechnen wir die Wahrscheinlichkeiten \(P(A),P(B),P(C)\) und \(P(D)\).

Wir versuchen zunächst eine Gleichung für \(P(A)\) aufzustellen.

Berechnen wir zunächst die Wahrscheinlichkeit für Variante 1): Die Wahrscheinlichkeit, dass jemand von Seite B auf A kommt ist: \(0,2\cdot P(B)\), von C auf A ist \(0,2\cdot P(C)\) und von D auf A ist \(0,1\cdot P(D)\). Damit ergibt sich für Möglichkeit 1):

\[0,2P(B)+0,2P(C)+0,1P(D) \]

Wie sieht es mit Variante 2) aus. Da es vier Webseiten gibt, ist die Wahrscheinlichkeit zufällig auf Seite 4 zu kommen: \(1/4\).

Insgesamt ergibt sich unter Berücksichtigung des Dampingfaktors \(d=0.85\) folgende Gleichung:

\[P(A)=0,85(0,2P(B)+0,2P(C)+0,1P(D) )+0,15\cdot 1/4 \]

Wenn wir das selbe für die Wahrscheinlichkeiten \(P(B)\),\(P(C)\) und \(P(D)\) machen bekommen wir folgendes System von Gleichungen:

\[\begin{split}P(A)&=0,85(0,2𝑃(𝐶)+0,2𝑃(𝐵)+0,1𝑃(𝐷))+0,15⋅0.25 \\ 𝑃(𝐵)&=0,85(0,5𝑃(𝐴)+0,6𝑃(𝐶)+0,8𝑃(𝐷))+0,15⋅0,25\\ 𝑃(𝐶)&=0,85(0,4𝑃(𝐴)+0,7𝑃(𝐵)+0,1𝑃(𝐷))+0,15⋅0,25\\ 𝑃(𝐷)&=0,85(0,1𝑃(𝐴)+0,1𝑃(𝐵)+0,2𝑃(𝐶))+0,15⋅0,25\end{split}\]

Das sind also 4 Gleichungen mit 4 Unbekannten.

Frage: Wie können wir ein solches System lösen. Genau damit wollen wir uns in diesem Kapitel beschäftigen.

Mit der Lösung von Linearen Gleichungssystemen mittels dem Gauß-Algorithmus.

4.3 Lineare Gleichungssysteme

In diesem Kapitel wollen wir formal einführen was ein lineares Gleichungssystem ist und wie dieses durch, sogenannte Matrizen, dargestellt werden kann.

Definition 39

Seien \(m,n\in \mathbb{N}\) Ein lineares Gleichungssystem mit \(n\) Unbekannten und \(m\) Gleichungen lässt sich wie folgt darstellen:

\[\begin{split}a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n &=b_1 \\ &\vdots \\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n &=b_m. \end{split}\]

Dabei sind \(x_1,\dots,x_n\) die Variablen des Systems und die \(a_{ij}\) die Koeffizienten.

Wir nennen \(A = \left( \begin{matrix} a_{11} & \dots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \dots & a_{mn} \end{matrix} \right)\) die Matrix des Systems und \((A,b)=\left( \begin{array}{ccc|c} a_{11} & \dots & a_{1n} & b_1 \\ \vdots & \ddots & \vdots & \vdots \\ a_{m1} & \dots & a_{mn} & b_m \end{array} \right)\) die erweiterte Koeffizientenmatrix.

Example 39

Betrachte das folgende lineare Gleichungssystem

\[\begin{split}x + 2y =& 1 \\ 3x + 4y =& 0.\end{split}\]

Dann ist \(A = \left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right)\) die Matrix des Systems und \((A,b)=\left( \begin{array}{cc|c} 1 & 2 & 1 \\ 3 & 4 & 0 \end{array} \right)\) die erweiterte Koeffizientenmatrix.

Definition 40

Ein Vektor \(v=\left(\begin{array}{c}v_1\\v_2\\ \vdots \\v_n\end{array}\right)\in \mathbb{R}^n\) heißt Lösung des Linearen Gleichungssystems. Falls das Einsetzen von \(v\) die Folgenden wahren Ausdrück produziert:

\[\begin{split}a_{11}v_1 + a_{12}v_2 + \dots + a_{1n}v_n &=b_1 \\ &\vdots \\ a_{m1}v_1 + a_{m2}v_2 + \dots + a_{mn}v_n &=b_m. \end{split}\]

Wir nennen die Mönge aller Lösungen die Lösungsmenge.

Example 40

Bestimmen Sie die Lösungsmenge des folgenden linearen Gleichungssystem

\[\begin{split}x + 2y =& 1 \\ 3x + 4y =& 0.\end{split}\]

Wir lösen zunächst die erste Gleichung nach \(x\) auf:

\[x =1-2y. (*)\]

Nun setzen wir diese Identität in die zweite Gleichung ein und erhalten:

\[3(1-2y)+4y=0.\]

Das vereinfacht sich zu:

\[3-6y+4y=0.\]

Dies können wir nun leicht nach \(y\) auflösen und erhalten:

\[y=3/2.\]

Setzen wir dies wieder in (*) ein, erhalten wir außerdem:

\[x=1-2\cdot 3/2=-2.\]

Die Lösungsmenge ist also:

\[\begin{split}L=\{\left(\begin{array}{c}-2 \\ 3/2 \end{array}\right)\}.\end{split}\]

Das war einfach aber was machen wir mit 3 Gleichungen mit 3 Unbekannten. Oder noch schlimmer was machen wir mit \(n\) Gleichungen und \(n\) Unbekannten? Dafür brauchen wir den Gauß-Algorithmus. Aber vorher schauen wir uns noch die Geometrische Interpretation von Linearen Gleichungssystem an.

## 4.4 Geometrische Interpretation von Linearen Gleichungssystemen

Lineare Gleichungssysteme haben neben der algebraischen Beschreibung auch eine intuitive geometrische Interpretation. Es gibt Grundsätzlich zwei verschiedene Geometrische Berschreibungen:

• Zeileninterpretation

• Spalteninterpretation

Zeileninterpretation

Als Beispiel betrachten wir das folgende Lineare Gleichungssystem

\[\begin{split}\color{green}2x - y =& 1 \\ \color {blue}x + y =& 5\end{split}\]

Beide Gleichungen können wir als Geraden in der Ebene interpretieren. Die Lösungsmenge können wir dann als Schnittpunktmenge der beiden Geraden interpretieren. Es ergibt sich also folgendes Bild.

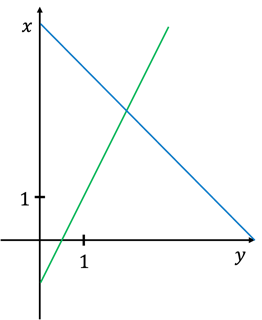
Durch diese Interpretation können wir direkt die Struktur der möglichne Lösungsmengen von zwei Gleichungen mit zwei Unbekannten ablesen:

1. Zwei Geraden schneiden sich: genaue eine Lösung

2. Zwei Gerade sind parallel aber nicht identisch: keine Lösung

3. Zwei Geraden sind identisch: unendlich viele Lösungen.

Spalteninterpretation

Eine weitere, aber weniger bekannte Beschreibung, ist die Spalteninterpretation. Dafür schreiben wir die beiden Gleichungen in Spaltenform um:

\[\begin{split}\color{green}x\cdot \begin{pmatrix} 2\\ 1 \end{pmatrix} + y \cdot \color{blue}\begin{pmatrix} -1\\ 1 \end{pmatrix} =\color{purple}\begin{pmatrix} 1 \\ 5 \end{pmatrix} \end{split}\]

Wir können nun die Lösungen interpretieren als die Vielfache die wir zu den Vektoren \(\begin{pmatrix} 2\\ 1 \end{pmatrix}\) und \(\begin{pmatrix} -1\\ 1 \end{pmatrix}\) multiplizieren müssen um auf den Punkt \(\begin{pmatrix} 1\\ 5 \end{pmatrix}\) zu kommen.

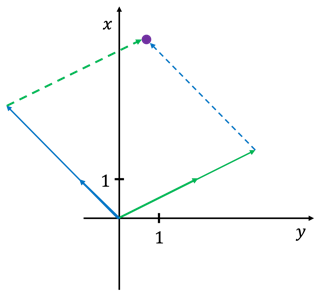
Auch mit dieser Interpretation können wir nun wieder die Lösungsmenge charakterisieren:

1. Zwei Vektoren haben verschiedene Richtungen: es gibt genau eine Lösung

2. Zwei Vektoren sind in der Gleichungen Richtung und der Punkt liegt nicht auf der Geraden: keine Lösung

3. Zwei Vektoren sind in der gleichen Richtung und der Punkt liegt auf der dadurch definierten Geraden: unendlich viele Lösungen.

4.5 Der Gauß-Algorithmus

Der Gauß Algorithmus ist ein Verfahren um systematisch die Lösungsmenge von linearen Gleichungssystemen zu bestimmen.

Der Gauß-Algorithmus basiert auf sogenannten elementaren Zeilenumformungen.

Definition 41

Sei \((A,b)=\left( \begin{array}{ccc|c} a_{11} & \dots & a_{1n} & b_1 \\ \vdots & \ddots & \vdots & \vdots \\ a_{m1} & \dots & a_{mn} & b_m \end{array} \right)\) die erweiterte Koeffizientenmatrix eines linearen Gleichungssystems.

Wir nennen die folgenden Operationen auf der erweiterten Koeffizientenmatrix eine elementare Zeilenumformung:

1. Vertauschung zweier Zeilen

2. Addition des 𝜆- fachen einer Zeile einer Zeile zu einer anderen Zeile (\(\lambda\in \mathbb{R}\)).

In Form von Gleichungen bedeutet 1) einfache nur die Reihenfolge der Gleichungen zu tauschen und 2) bedeutet, dass wir zwei Gleichungen addieren und eine neue Gleichung dadurch entsteht.

Die Wichtige Erkenntnis ist nun, dass beide Umformungen die Lösungsmenge des Systems nicht ändern.

Wir haben daher folgenden Satz:

Theorem 18

Sei \((𝐴,𝑏)\) die erweiterte Koeffizientenmatrix eines lineares Gleichungssystems und \((\tilde{𝐴},\tilde{𝑏} )\) ein weiteres Gleichungssystem, dass durch elementare Zeilenumformung aus \((𝐴,𝑏)\) entsteht. Dann haben beide Gleichungssystem, die gleiche Lösungsmenge.

Der Gauß Algorithmus ist nun ein Verfahren welches die erweiterte Koeffizientenmatrix unter Zuhilfenahme von elementaren Zeilenumformungen soweit vereinfacht, dass wir das System lösen können.

Ziel des Gauß-Verfahrens

Das Ziel des Verfahrens ist es, dass nach Anwendung der elementaren Zeilenumformungen, die erweiterte Koeffizientenmatrix die folgende Form besitzt:

\[\begin{split}\left(\begin{array}{ccccc|c} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} & b_1 \\ 0 & a_{22} & a_{23} & \cdots & a_{2n} & b_2 \\ 0 & 0 & a_{33} & \cdots & a_{3n} & b_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & a_{nn} & b_n \end{array}\right)\end{split}\]

Wir werden im nächsten Abschnitt anhand der Beispiele sehen, wie man zu so einer Form gelangt und wie man dann das LGS lösen kann.

Beispiele für den Gauß-Algorithmus

Wir wollen zunächst den Fall betrachten, wenn der Gauß-Algorithmus erfolgreich durchgeführt werden kann. Hierfür betrachten wir den Fall, dass wir \(n\) Gleichungen mit \(n\) Unbekannten haben. Also gleich viele Gleichungen wie Unbekannte.

Wir betrachten das Beispiel:

Example 41

Es sei folgendes Lineares Gleichungssystem gegeben:

\[\begin{split}u+2v+w &=2\\ 3u+8v+w&=12\\ 4v+w&=2.\end{split}\]

Die Lösung mittels Gauß Algorithmus wird in dem folgendem Video beschrieben:

Und noch ein Beispiel:

Example 42

Es sei folgendes Lineares Gleichungssystem gegeben:

\[\begin{split}2u-3v-w &=1\\ 2v+3w&=11\\ 4u+2v+3w&=6.\end{split}\]

Die Beschreibung des Gauß-Algorithmus und weitere Beispiele finden Sie auch hier: Klick mich .

Die Edgecases - Reparierbarer und nicht reparierbarer Fall.

Der Algorithmus so wie wir ihn gesehen haben kann fehlschlagen wenn wir in einem Diagonelement eine \(0\) stehen haben. Dann können wir kein Vielfaches dieser Zeile zu einer weiteren addieren um die Zahlen unterhalb dieses Diagonalelements zu null zu machen.

Es kann jedoch sein, dass dieser Fall reparierbar ist, in dem wir Zeilen vertauschen.

Dafür betrachten wir das folgende Beispiel:

Example 43

Es sei folgendes Lineares Gleichungssystem gegeben:

\[\begin{split}u+v+w &=1\\ 2u+2v+5w&=2\\ 4u+6v+8w&=6.\end{split}\]

Betrachten Sie nun das folgende Video:

Es kann leider aber auch vorkommen, dass wir durch vertauschen von zwei Zeilen den Algorithmus nicht reparieren können. Dafür betrachten wir das folgende Beispiel.

Example 44

Es sei folgendes Lineares Gleichungssystem gegeben:

\[\begin{split}u+v+w &=1\\ 2u+2v+5w&=2\\ 4u+4v+8w&=6.\end{split}\]

Betrachten Sie nun das folgende Video:

Der Allgemeine Fall

Wir wollen nun im letzten Schritt eine Allgemeine Beschreibung der Lösungsmenge von linearen Gleichungssystemen geben.

Dafür müssen wir zunächst die Folgenden Definitionen vornehmen.

Definition 42

Eine Matrix \(A\) ist eine Zeilenstufenform falls es von der folgenden Gestalt ist. 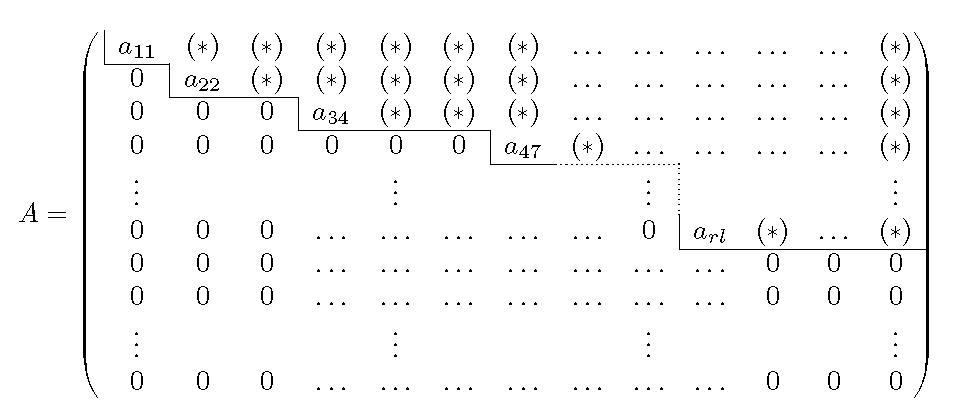wobei die mit (*) markierten Einträge \(\neq 0\) sind. Wir nennen die Zahl \(r\in \mathbb{N}\) den Rang der Matrix.

Die Definition ist weniger kompliziert als es zunächst aussehen mag. Wir meinen lediglich das wenn wir eine Trennline zwischen Einträgen, die nicht 0 sind und den Nulleinträgen wie eine Treppe verläuft. Also entweder runter geht oder gerade bleibt. Dabei kanne die Treppenstufe beliebig lang sein.

Ein wichtiger Spezialfall, den wir bereits gesehen haben sind sogenannte obere Dreiecksmatrizen. Diese sind wie folgt definiert.

Definition 43

Wir nennen eine Matrix, mit der folgenden Form eine obere Dreiecksmatrix

\[\begin{split}\left( \begin{array} a a_{1,1} & a_{1,2} & a_{1,3} & \dots & a_{1,n-1} & a_{1,n} \\ 0 & a_{2,2} & a_{2,3} & \dots & a_{2,n-1} & a_{2,n} \\ 0 & 0 & a_{3,3} & \dots & a_{3,n-1} & a_{3,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \dots & a_{n-1,n-1} & a_{n-1,n} \\ 0 & 0 & 0 & \dots & 0 & a_{n,n} \end{array}\right),\end{split}\]

wobei die \(a_{ii}\neq 0\).

Remark 2

Jede obere Dreiecksmatrix ist insbesondere eine Matrix in Zeilenstufenform

Wir sind nun in der Lage einen allgemeinen Satz zu formulieren welches Ergebnis der Gauß-Algorithmus in jedem Fall liefert.

Theorem 19

Sei \((𝐴,𝑏)\) die erweiterte Koeffizientenmatrix eines linearen Gleichungssystems. Dann existiert eine endliche Kette von elementaren Zeilenumformungen, so dass das transformierte System \((\tilde{𝐴} ,\tilde{𝑏} )\) die Eigenschaft hat, dass \(\tilde{𝐴}\)  Zeilenstufenform besitzt.

Anders ausgedrückt besagt der obige Satz, dass das Ergebnis einer Matrix nach dem Gauß-Algorithmus stets Zeilenstufenform besitzt.

Nun können wir den allgemeinen Fall beschreiben:

Nehmen wir an wir haben ein erweiterte Koeffizientenmatrix \((A,b)\), wobei \(A\) Zeilenstufenform besitzt. Dann haben wir die folgende Situation

.

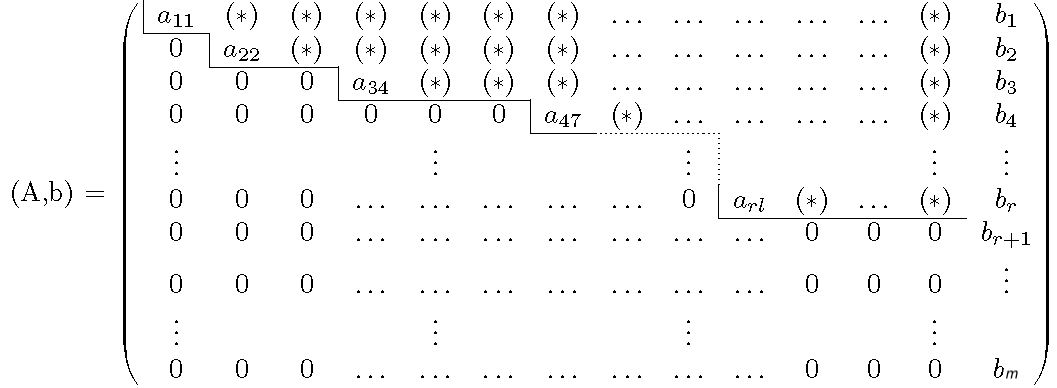Wir haben nun mehrere Fälle, die wir unterscheiden:

Fall 1 \(A\) ist eine obere Dreiecksmatrix. Dann besteht die Lösungsmenge aus einer Lösung

Fall 2.1 \(A\) ist keine obere Dreicksmatrix und eine der Zahlen \(b_{r+1},\dots , b_m \neq 0\). Dann gibt es keine Lösung,da dann die Gleichung niemals erfüllt sein kann.

Fall 2.2 \(A\) ist keine obere Dreicksmatrix und \(b_{r+1}=b_{r+2}=\dots = b_m=0\) so sind die Gleichung stets erfüllt und wir erhalten unendlich viele Lösungen oder genau eine Lösung.

Frage: Überlegen Sie sich für den Fall 2.2, eine Situation in der es genau eine Lösung gibt. Antwort:

Betrachten Sie zum Beispiel das Gleichungssystem mit :

\[\begin{split}\begin{cases} 2x_1 - x_2 + 3x_3 = 5 \\ 3x_2 - 4x_3 = 6 \\ 2x_3 = 1 \\ 2x_1 - x_2 + 3x_3 = 5 \\ \end{cases}\end{split}\]

Dies führt mittels Gauß (letzte Gleichung ist gleich der ersten Gleichung) zu folgender Koeffizientenmatrix:

\[\begin{split}\left(\begin{array}{ccc|c} 2 & -1 & 3 & 5 \\ 0 & 3 &-4 & 6 \\ 0 & 0& 2 & 1 \\ 0 & 0 & 0 & 0 \\ \end{array}\right)\end{split}\]

Dieses Gleichungssystem entspricht aber einem Gleichungssystem in oberer Dreiecksform mit 3 Gleichungen und 3 Unbekannten und ist daher eindeutig lösbar.

Insgesamt ergibt sich der folgende Satz.

Theorem 20

Gegeben sein ein lineares Gleichungssystem mit \(m\) Gleichungen und \(n\) Unbekannten mit einer erweiterten Koeffizientenmatrix \(B=(A,b)\), wobei \(A\) die Matrix des Systems ist. Dann gibt es die folgenden Fälle:

• Fall 1: \(A\) ist eine obere Dreiecksmatrix: In diesem Fall besteht die Lösungsmenge aus genau einem Element.

• Fall 2.1 \(A\) ist keine obere Dreiecksmatrix, es gilt \(r<m\) und es gibt ein \(b_k\neq 0\) für ein \(k\in \left\{r+1,\dots , m\right\}\). Dann gibt es keine Lösung.

• Fall 2.2 \(A\) ist keine obere Dreiecksmatrix und es gilt entweder \(r=m\) oder \(b_{r+1}=b_{r+2}=\dots = b_m=0\). Dann gibt es unendlich viele Lösungen oder genau eine Lösung.

Das ganze wollen wir nun noch an zwei Beispielen illustrieren.

Example 45

Beschreibe die Lösungsmenge des folgenden Linearen Gleichungssystems:

\[\begin{split}x-z&=0 \\ y+2z&=0\end{split}\]

Example 46

Wir schauen uns nun nochmal das folgende Gleichungssystem an

\[\begin{split}u+v+w &=1\\ 2u+2v+5w&=2\\ 4u+4v+8w&=6.\end{split}\]