Kapitel 5 – Matrizen#
5.1 Lernziele#
In diesem Abschnitt lernen wir die folgenden Dinge:
Lernziele
Verständnis der Matrixnotation und des Aufbaus von Matrizen
Beherrschung grundlegender Operationen mit Matrizen wie Addition, Subtraktion, skalarer Multiplikation und Transposition
Verständnis der Matrixmultiplikation, einschließlich der Bedingungen für ihre Durchführung und der Eigenschaften der Matrixmultiplikation
5.2 Was ist eine Matrix – z. B. ein Graustufenbild?#
Eine Matrix ist nichts Kompliziertes. Im Wesentlichen handelt es sich um eine tabellarische Anordnung von Zahlen mit Spalten und Zeilen, die wir in runde Klammern setzen. Das kann so aussehen:
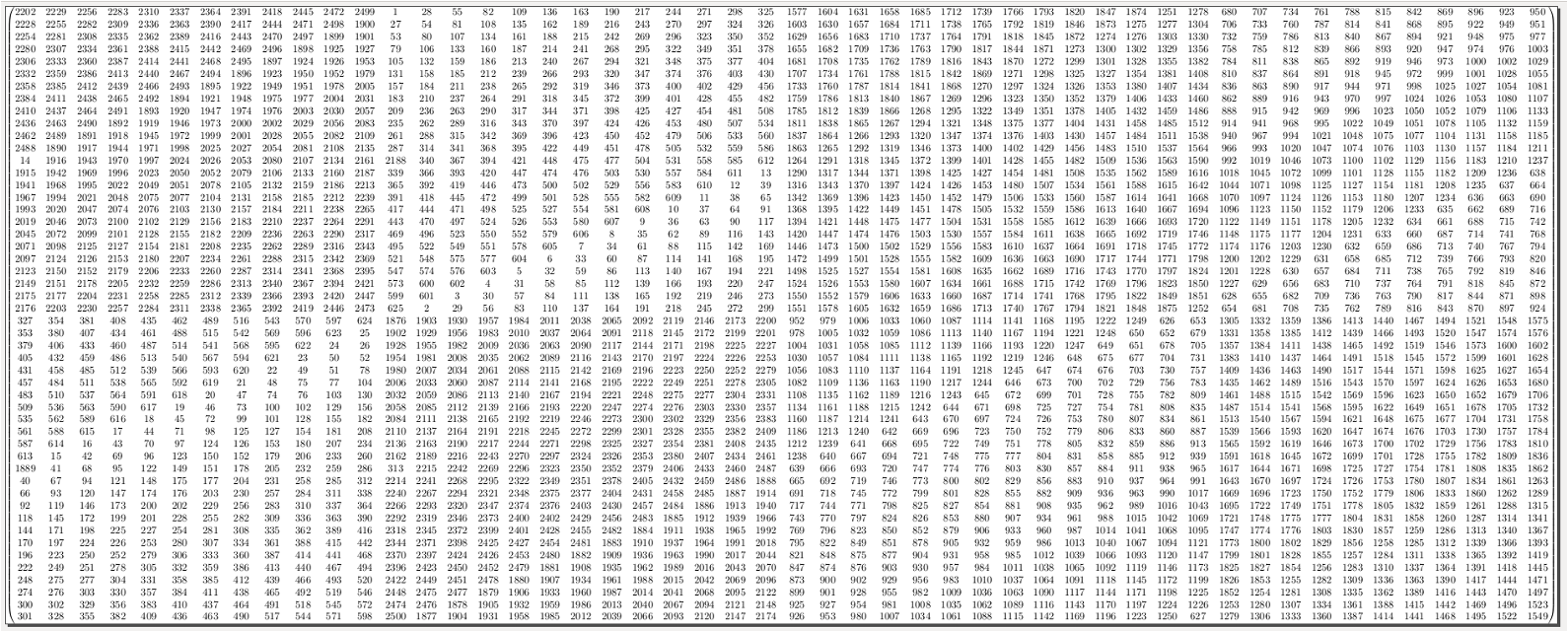
Oder aber wenn wir es mit vielen Daten zu tun haben auch mal so:
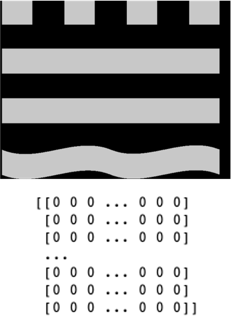
Matrizen spielen eine wichtige Rolle, immer wenn es um Daten geht. So lassen sich Datentabellen als Matrizen interpretieren, wenn die Werte nur aus Zahlen bestehen. Matrizen spielen ebenso in der Bildverarbeitung eine wichtige Rolle – am einfachsten wird dies bei Graustufenbildern sichtbar.
Die Pixel des Bildes ergeben die tabellarische Anordnung. Der Wert wird durch die Intensität des einzelnen Pixels gegeben.
So ergibt beispielsweise folgendes Bild:

Folgende Matrix:

Skalare Multiplikation
Wir können nun das Bild bearbeiten, indem wir die Matrix verändern. Beispielsweise können wir jeden Wert mit 2 multiplizieren:

Was bedeutet diese Operation auf der Ebene des Bildes?
Es ist eine Erhöhung des Kontrasts:

Matrixaddition Sei nun ein weiteres Bild gegeben:
Wir nehmen nun weiter an, dass beide Bilder und damit auch die zugehörigen Matrizen die gleiche Größe besitzen.
Wir wollen nun beide Bilder übereinanderlegen. Dies erreichen wir durch Addition der beiden entsprechenden Matrizen. Das heißt, in jeder Komponente addieren wir die beiden Zahlen miteinander, sodass eine neue Matrix derselben Größe entsteht.

5.3 Matrixnotation#
In diesem Kapitel machen wir uns mit der Matrixschreibweise vertraut und führen einige formale Notationen ein.
Matrizen#
Wir verwenden als Namen für Matrizen häufig Großbuchstaben. Zum Beispiel
Die Matrix \(B\) hat 2 Zeilen und 3 Spalten. Wir nennen sie eine \(2\times 3\)-Matrix.
Wir schreiben eine allgemeine \(m\times n\)-Matrix wie folgt:
Wir nennen \(m\times n\) die Dimension der Matrix \(A\).
Obige Struktur bedeutet, dass wenn wir für eine Matrix \(A\) den Wert \(a_{ij}\) schreiben, dass wir den Wert in der \(i\)-ten Zeile und der \(j\)-ten Spalte meinen.
Frage
Im obigen Beispiel: Was ist \(b_{12}\)?
Antwort:
\(b_{12}=3\)
Im nächsten Schritt müssen wir definieren, welchen Wertebereich die einzelnen Zahlen in der Matrix haben sollen. In der Regel wollen wir, dass die Zahlen in \(\mathbb{R}\) sind.
Wir schreiben für die Menge aller möglichen \(m\times n\)-Matrizen mit reellen Einträgen:
Vektoren#
Eine \(n\times 1\)-Matrix nennen wir Spaltenvektor oder Vektor. Zum Beispiel \(v=\begin{pmatrix} 1\\2\\3\\4 \end{pmatrix}\). Wir schreiben statt \(\mathbb{R}^{n\times 1}\) einfach nur \(\mathbb{R}^n\).
Eine \(1\times n\)-Matrix nennen wir Zeilenvektor. Zum Beispiel \(v=\begin{pmatrix} 1 & 2 & 3 & 4 \end{pmatrix}\).
Spalten- und Zeilenvektoren bezeichnen wir in der Regel mit einem kleinen lateinischen Buchstaben (z. B. \(v,w,u\)).
Skalar#
Falls wir im Kontext der Matrizen- und Vektorrechnung betonen wollen, dass es sich bei einem Objekt um eine einzige Zahl (z. B. aus \(\mathbb{R}\)) handelt, nennen wir es einen Skalar. Wir schreiben dann häufig einen kleinen griechischen Buchstaben, um das zu kennzeichnen (z. B. \(\lambda \in \mathbb{R}\)).
Besondere Matrizen#
Wir wollen noch zwei besondere Matrizen einführen, die es verdienen, eine abkürzende Schreibweise zu bekommen.
Zunächst die Nullmatrix: \(\mathbf{0}_{m n}\in \mathbb{R}^{m\times n}\). Dies bezeichnet eine \(m\times n\)-Matrix, die nur aus Nullen besteht. Ist der Kontext klar, schreiben wir kurz \(\mathbf{0}\).
Zum Anderen die sogenannte Einheitsmatrix.
Dies ist eine spezielle Matrix, bei der die Diagonalelemente 1 sind und alle anderen Elemente 0.
5.4 Skalare Multiplikation und Matrixaddition#
Die skalare Multiplikation und die Matrixaddition sind fundamentale Rechenoperationen für Matrizen. Wir beginnen mit der Matrixaddition.
Matrixaddition#
Definition 44
Gegeben seien zwei Matrizen \(A,B\in \mathbb{R}^{m\times n}\) mit derselben Dimension \(m \times n\). Die Addition von \(A\) und \(B\), dargestellt als \(A + B\), ergibt eine neue Matrix \(C\) der gleichen Dimension \(m \times n\), wobei jedes Element \(c_{ij}\) in \(C\) definiert ist als:
Machen wir dazu ein einfaches Beispiel.
Example 47
Skalare Multiplikation#
Definition 45
Sei \(A \in \mathbb{R}^{m\times n}\) und \(\lambda\in \mathbb{R}\) ein Skalar. Dann ist \(C=\lambda A\) definiert durch
Machen wir dazu ein einfaches Beispiel.
Example 48
Sei \(A\) eine \(2 \times 3\)-Matrix und \(\lambda = 3\) ein Skalar. Die skalare Multiplikation von \(A\) mit \(\lambda\) ergibt:
Rechengesetze der Addition und skalaren Multiplikation#
Seien \(A,B,C\in \mathbb{R}^{m\times n}\), sowie \(\lambda,\mu\in \mathbb{R}\).
Dann gelten folgende Rechenregeln:
Matrixaddition:
Kommutativgesetz: \(A + B = B + A\)
Assoziativgesetz: \((A + B) + C = A + (B + C)\)
Nullmatrix: \(A + \mathbf{0} = A\)
Negation: \(A + (-A) = \mathbf{0}\)
Skalare Multiplikation:
Assoziativgesetz: \((\lambda \mu)A = \lambda(\mu A)\)
Distributivgesetz (Skalar): \((\lambda + \mu)A = \lambda A + \mu A\)
Distributivgesetz (Matrix): \(\lambda (A + B) = \lambda A + \lambda B\)
Einheitselement: \(1\cdot A = A\)
Null: \(0\cdot A = \mathbf{0}\)
5.5 Transposition von Matrizen#
Das Transponieren einer Matrix vertauscht Zeilen und Spalten. Aus einer \(m\times n\)-Matrix wird eine \(n\times m\)-Matrix \(A^T\). Genauer definieren wir:
Definition 46
Sei \(A\in \mathbb{R}^{m\times n}\). Dann ist \(C=A^T\) die \(n\times m\)-Matrix mit
Example 49
Sei
Die Transposition von \(A\) erhalten wir, indem wir die Zeilen von \(A\) zu den Spalten von \(A^T\) und die Spalten von \(A\) zu den Zeilen von \(A^T\) machen:
Frage: Was ist die doppelte Transposition einer Matrix: \((A^T)^T\)?
Antwort:
\((A^T)^T=A\)
5.6 Matrixmultiplikation#
Bisher haben wir Addition und skalare Multiplikation komponentenweise definiert. Die Multiplikation zweier Matrizen funktioniert anders. Wir bauen sie schrittweise auf.
Vektor mal Vektor#
Die einfachste Möglichkeit einer Matrixmultiplikation ist die Multiplikation eines Zeilenvektors mit einem Spaltenvektor. Dies entspricht dem aus der Analytischen Geometrie bekannten Skalarprodukt.
Sei dazu \(v=\begin{pmatrix} a_1 & a_2 & \dots & a_n \end{pmatrix}\in \mathbb{R}^{1\times n}\) und \(w=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}\in \mathbb{R}^{n\times 1}\).
Dann definieren wir:
Example 50
Sei
Das Skalarprodukt wird berechnet, indem die entsprechenden Elemente der beiden Vektoren multipliziert und summiert werden:
Matrix mal Vektor#
Die Situation “Matrix mal Vektor” hatten wir schon im Kapitel Lineare Gleichungen.
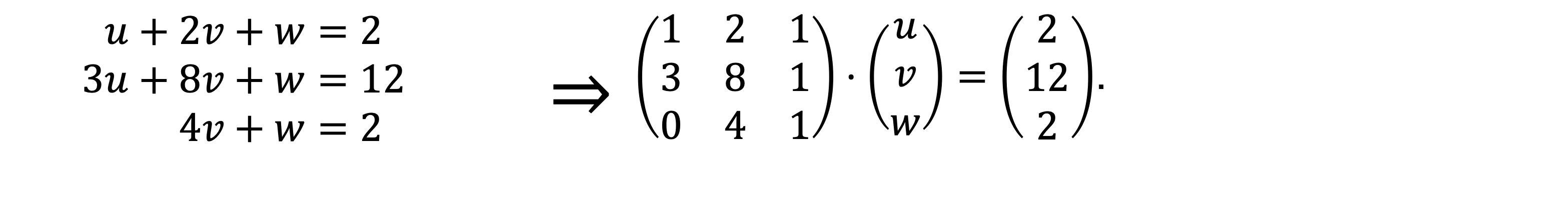
Wir sehen, dass beim Produkt Matrix mal Vektor ein neuer Vektor entsteht; seine Komponenten sind die Skalarprodukte der Zeilen von \(A\) mit \(v\).
Formal ausgedrückt heißt das:
Sei \(A\in \mathbb{R}^{m\times n}\) und \(v\in \mathbb{R}^{n\times 1}\).
Dann ist \(w=A\cdot v \in \mathbb{R}^{m\times 1}\) und es gilt:
wobei \(a_{i*}\in \mathbb{R}^{1\times n}\) die \(i\)-te Zeile von \(A\) ist.
Auch hierzu gucken wir uns ein kurzes Beispiel an
Example 51
Angenommen, wir haben die Matrix \(A\) und den Vektor \(v\) gegeben:
Um die Multiplikation von \(A\) und \(v\) durchzuführen, multiplizieren wir jede Zeile von \(A\) mit dem entsprechenden Element von \(v\) und summieren die Produkte. Das Ergebnis ist ein neuer Vektor \(w\):
Das Ergebnis der Multiplikation von \(A\) und \(v\) ist der Vektor \(w = \begin{pmatrix} 20 \\ 47 \end{pmatrix}\). Beachte, dass die Anzahl der Spalten in \(A\) der Anzahl der Zeilen in \(v\) entsprechen muss, um die Multiplikation durchführen zu können.
Matrix mal Matrix#
Als letztes betrachten wir nun das Produkt zweier Matrizen \(A\) und \(B\).
Die erste Frage lautet: Welche Dimensionen dürfen \(A\) und \(B\) haben, damit \(AB\) definiert ist?
Die obige Formel beschreibt dies. Demnach muss die Anzahl der Spalten der ersten Matrix mit der Anzahl der Zeilen der zweiten Matrix übereinstimmen.
Aber wie berechnet man das Produkt von zwei Matrizen:
Definition 47
Sei \(A\in \mathbb{R}^{m\times n}\) und \(B\in \mathbb{R}^{n\times k}\). Dann ist das Produkt \(C=AB\) definiert durch
Dabei ist \(a_{i*}\in \mathbb{R}^{1\times n}\) die \(i\)-te Zeile von \(A\) und \(b_{*j}\in\mathbb{R}^{n\times 1}\) die \(j\)-te Spalte von \(B\).
Das heißt, das Produkt \(AB\) ist die Matrix \(C\), deren \((i,j)\)-Eintrag das Skalarprodukt der \(i\)-ten Zeile von \(A\) mit der \(j\)-ten Spalte von \(B\) ist.
Hier noch ein einfaches Beispiel
Example 52
Angenommen, wir haben die Matrix \(A\) der Dimension \(2\times 3\) und die Matrix \(B\) der Dimension \(3\times 2\):
Um das Produkt \(AB\) zu berechnen, multiplizieren wir jede Zeile von \(A\) mit jeder Spalte von \(B\) und summieren die entsprechenden Produkte. Das Ergebnis ist eine neue Matrix \(C\) der Dimension \(2\times 2\):
Es gibt auch viele gute externe Quellen, die einem gut erklären, wie man zwei Matrizen miteinander multiplizieren kann.
Z.B.
5.7 Gesetze der Matrixmultiplikation#
Es seien \(A,B,C\) Matrizen geeigneter Dimensionen und \(\lambda\in \mathbb{R}\). Dann:
\((A B) C = A (B C) = A B C\)
\((\lambda A) B = A (\lambda B) = \lambda (A B)\)
\(A E = E A = A\)
\(A \mathbf{0} = \mathbf{0} A = \mathbf{0}\)
\(A (B + C) = A B + A C\)
\((A + B) C = A C + B C\)
\((A B)^T = B^T A^T\)
Achtung: Im Allgemeinen gilt
Es existiert also kein Kommutativgesetz für Matrizen.